Triangles (त्रिभुज)
Get “Triangles” chapter’s previous years questions from 2009 to 2020 of JAC board.
Q1. All the squares are – congruent or similar?
{ सभी वर्ग होते है – सर्वांगसम या समरूप?}
Ans. Similar
{समरूप}
Q2. Are all triangles similar – equilateral or isosceles?
{ क्या सभी त्रिभुज समरूप होते है – समबाहु या समद्विबाहु?}
Ans. equilateral
{समबाहु )
Q3. All the circles are – congruent or similar?
{ सभी वृत्त होते है – सर्वांगसम या समरूप?}
Ans. Similar
{समरूप}
Q4. 2 polygons of the same number of sides are similar if their corresponding sides are…
{ भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते है| यदि उनकी संगत भुजाएं … हों|} Ans. Proportional
{आनुपातिक}
Q5. In figure, if DE||BC , then find the value of x
{आकृति में यदि DE||BC है| तो x का मान लिखिए|} 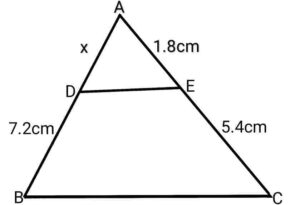 Ans. From Thales theorem,
Ans. From Thales theorem,
{थेल्स प्रमेय से,
}
Q6. In the figure , DE||BC. If and AC = 4.8cm, find AE.
{आकृति में DE||BC है| यदि और AC = 4.8cm| तो AE ज्ञात कीजिये|}
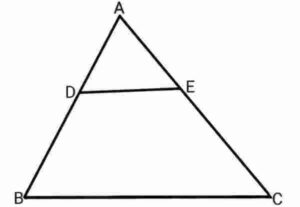
Ans. From Thales theorem,
3 × 4.8 - 3AE = 5AE
8AE = 14.4
AE = 1.8cm
{थेल्स प्रमेय से,
3 × 4.8 - 3AE = 5AE
8AE = 14.4
AE = 1.8cm}
Q7. In the given figure DE||BC. Find x
{नीचे आकृति में DE||BC यदि है, x निकालिये}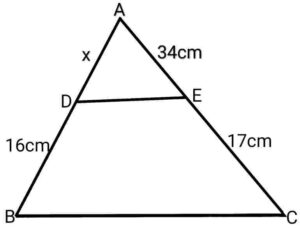
Ans. From Thales theorem,
cm
{थेल्स प्रमेय से,
cm}
Q8. In the given figure DE||BC. Find x
{नीचे आकृति में DE||BC यदि है, x निकालिये}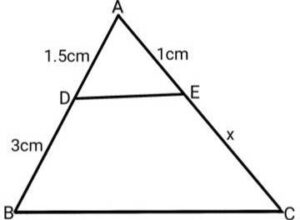
Ans. From Thales theorem,
x = 2cm
{थेल्स प्रमेय से,
x = 2cm}
Q9. Say the pair of triangles in the given figure are similar or not. If yes, state the similarity criterion used by you for answering the question. Also write the pair of similar triangles in the symbolic form
{ बताइए की आकृति में दिए गए त्रिभुजों के युग्म समरूप है या नहीं| यदि है तो उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है| साथ ही समरूप त्रिभुज के जोड़े को सांकेतिक रूप में व्यक्त कीजिए|}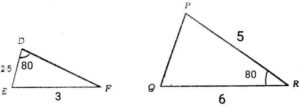
Ans. The pair of triangles are not similar.
{त्रिभुजों के युग्म समरूप नहीं है|}
Q10. Say the pair of triangles in the given figure are similar or not. If yes, state the similarity criterion.
{ बताइए की आकृति में दिए गए त्रिभुजों के युग्म समरूप है या नहीं| यदि है तो उस समरूपता कसौटी को लिखिए}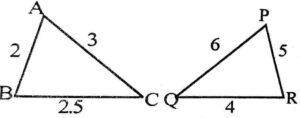
Ans. ,
and
Yes, by SSS similarity criterion ∆ABC~∆QRP
{ ,
और
हाँ , SSS समरूपता कसौटी से ∆ABC~∆QRP}
Q11. Say the pair of triangles in the given figure are similar or not. If yes, state the similarity criterion used by you for answering the question. Also write the pair of similar triangles in the symbolic form
{ बताइए की आकृति में दिए गए त्रिभुजों के युग्म समरूप है या नहीं| यदि है तो उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है| साथ ही समरूप त्रिभुज के जोड़े को सांकेतिक रूप में व्यक्त कीजिए|}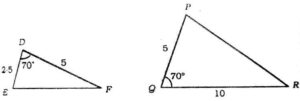
Ans. ∠D=∠Q=70°,
and
Yes, by SAS similarity criterion ∆EDF~∆PQR
{ ∠D=∠Q=70°,
and
हाँ , SAS समरूपता कसौटी से ∆EDF~∆PQR}
Q12. ABC is a isosceles triangle right angled at C. Prove That
{ABC एक समद्विबाहु त्रिभुज है जिसका कोण C समकोण है| सिद्ध कीजिए कि .}
Ans. Given:- ΔABC is an isosceles right triangle in which ∠C = 90°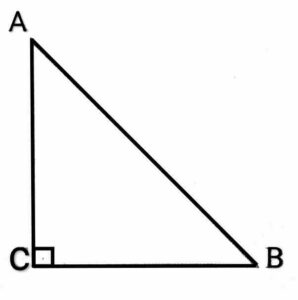 To prove:-
To prove:-
Proof:- AC=BC and ∠C = 90°
Now, by Phythagoras Theorem
(
AC=BC)
∴
{ दिया हुआ है:- ΔABC एक समद्विबाहु समकोण त्रिभुज है, जिसका कोण C समकोण है|

सिद्ध करना है:-
प्रमाण:- ∠C = 90° तथा AC=BC
अब, पाइथागोरस प्रमेय से
(
AC=BC)
∴ }
Q13. ABC is a isosceles triangle with AC=BC. If then prove that ABC is a right triangle.
{ABC एक समद्विबाहु त्रिभुज है जिसमें AC=BC है| यदि है, तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है}
Ans. Given:- ΔABC is an isosceles triangle in which AC=BC and 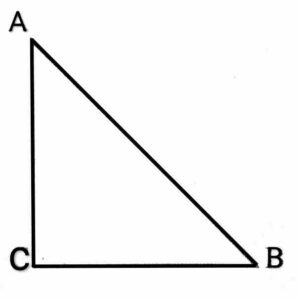 To Prove:- ABC is a right angled triangle
To Prove:- ABC is a right angled triangle
Proof:- AC=BC and
Now,
[AC=BC, given]
This side satisfied the Pythagoras theorem
∴ ABC is a right angled triangle
{दिया हुआ है:- ΔABC एक समद्विबाहु त्रिभुज है, जिसमे AC=BC और  सिद्ध करना है:- ABC एक समकोण त्रिभुज है
सिद्ध करना है:- ABC एक समकोण त्रिभुज है
प्रमाण:- AC=BC और
अब,
[AC=BC, दिया हुआ है]
यह पक्ष पाइथागोरस प्रमेय को संतुष्ट करता है|
∴ ABC एक समकोण त्रिभुज है जो C पर समकोण है|}
Q14. D is a point on the side BC of a triangle ABC in such a way that ∠ADC=∠BAC. So that .
{एक त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि ∠ADC=∠BAC है| सिद्ध कीजिये की }
Ans.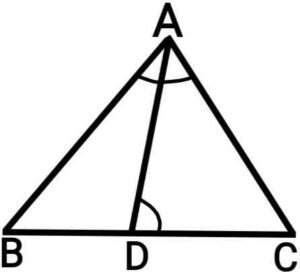 In ΔADC and ΔBAC
In ΔADC and ΔBAC
∠ADC=∠BAC (given)
∠ACD=∠ACB (common)
By AA similarity criterion
ΔADC∼ΔBAC
(prove)
{ ΔADC और ΔBAC में
ΔADC और ΔBAC में
∠ADC=∠BAC (दिया हुआ है)
∠ACD=∠ACB (उभयनिष्ठ कोण)
AA समरूपता कसौटी से,
ΔADC∼ΔBAC
(सिद्ध हो गया) }
Q15. Let ΔABC∼ΔDEF and their areas are and
respectively. If BC=11.2cm, find EF.
{माना लीजिये ΔABC∼ΔDEF हैं और उनके क्षेत्रफल क्रमशः और
हैं| यदि BC=11.2cm है, तो EF ज्ञात कीजिए|}
Ans. 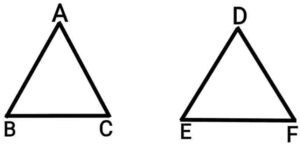 ΔABC∼ΔDEF
ΔABC∼ΔDEF
EF=15.4cm
Q16. If the areas of two similar triangles are equal, prove that they are congruent.
{यदि दो समरूप त्रिभुजों के क्षेत्रफल बराबर हों तो सिद्ध कीजिए कि वे त्रिभुज सर्वांगसम होते हैं|}
Ans. ΔABC∼ΔDEF
ΔABC∼ΔDEF
Given, ar(ABC)=ar(DEF)
By SSS congruency criterion,
ΔABC≅ΔDEF
{ ΔABC∼ΔDEF
ΔABC∼ΔDEF
दिया हुआ है, ar(ABC)=ar(DEF)
SSS सर्वांगसमता कसौटी से,
ΔABC≅ΔDEF}
Q17. Diagonals of a trapezium ABCD with AB||DC intersect one another at point O. If AB=2CD, find out the ratio of the areas of triangles AOB and COD.
{एक समलंब ABCD जिसमें AB||DC है के विकर्ण परस्पर बिंदु O पर प्रतिच्छेद करते हैं यदि AB=2CD हो, तो तिभुजों AOB और COD के क्षेत्रफलों का अनुपात ज्ञात कीजिए|}
Ans. 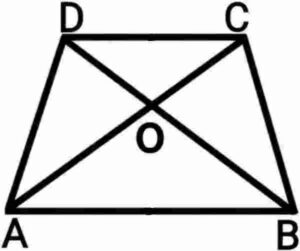 Given:- AB=2CD
Given:- AB=2CD
In ΔAOB and ΔCOD,
AB||DC
By alternate interior angle
∠BAO=∠DCO
and ∠ABO=∠CDO
By AA similarity criterion,
ΔAOB∼ΔCOD
{ दिया हुआ है:- AB=2CD
दिया हुआ है:- AB=2CD
ΔAOB and ΔCOD में,
AB||DC
एकांतर आंतरिक कोण से
∠BAO=∠DCO
and ∠ABO=∠CDO
AA समरूपता कसौटी से,,
ΔAOB∼ΔCOD
}
Q18. ABC and BDE are two equilateral triangles in such a way that D is the midpoint of BC. Find the ratio of the areas of the triangles ABC and BDE.
{ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्यबिंदु है| त्रिभुजों ABC और BDE के क्षेत्रफलों का अनुपात ज्ञात कीजिए|}
Ans.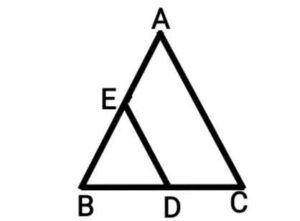
D is the mid point of BC.
ΔABC and ΔBDE are equilateral triangles
By AAA similarity criterion,
ΔABC∼ΔBDE
{ BC पर D मध्य बिंदु है|
BC पर D मध्य बिंदु है|
ΔABC और ΔBDE समबाहु त्रिभुज हैं
AAA समरूपता कसौटी से,
ΔABC∼ΔBDE
}
Q19. Prove that if a line is drawn parallel to one side of triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
{सिद्ध कीजिए कि यदि किसी त्रिभुज की एक भुजा के समांतर अन्य दो भुजाओ को भिन्न-भिन्न बिंदुओं पर प्रतिच्छेद करने के लिए एक रेखा खींची जाए, तो यह अन्य दो भुजाएं एक ही अनुपात में विभाजित हो जाती है|}Ans. Let ABC is a triangle in which DE||BC 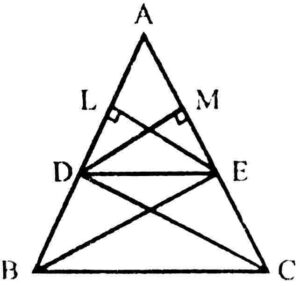
To prove:-
Construction:- Join BE , CD and then draw EL⊥AB, DM⊥AC
Proof:-
...(1)
Again,
...(2)
Here, ΔECD and ΔDBE are on the same base DE and between same parallel lines BC and DE.
ar(ECD) = ar(DBE) ...(3)
Putting this value in equation (2)
[
ar(AED = ar(ADE)]
∴
{माना की ABC एक त्रिभुज है, जिसमे DE||BC
सिद्ध करना है की:-
रचना:- EL⊥AB, DM⊥AC , BE और CD को मिला दिया|
प्रमाण:-
...(1)
इसी प्रकार,
...(2)
यहाँ, ΔECD और ΔDBE एक ही आधार DE पर और समान समानांतर रेखाओं BC और DE के बीच स्थित हैं।
ar(ECD) = ar(DBE) ...(3)
मूल्य को समीकरण (2) में रखने पर
[
ar(AED = ar(ADE)]
∴ }
Q20. Prove that in a right triangle , the square of the hypotenuse is equal to the sum of the squares of the other two sides.
{सिद्ध कीजिए कि एक समकोण त्रिभुज में कर्ण का वर्ग शेष 2 भूजाओ के वर्गों के योग के बराबर होता है|} Ans. Let ABC is a triangle in which ∠B = 90° and AC is a hypotenuse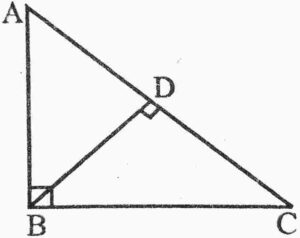 To prove:-
To prove:-
Construction:- BD⊥AC
Proof:- In right triangle ADB and ABC
∠ADB = ∠ABC = 90°
∠DAB = ∠BAC (common)
From AA similarity criterion ΔADB~ΔABC
∴
...(1)
Again in right triangle CDB and CBA
∠CDB = ∠ABC = 90°
∠BCD = ∠ACB (common)
From AA similarity criterion ΔCDB~ΔCBA
∴
...(2)
Equation (1) + equation (2)
∴
{ माना की ABC एक समकोण त्रिभुज है, जिसमे ∠B = 90° तथा कर्ण AC है| सिद्ध करना है की:-
सिद्ध करना है की:-
रचना:- B से AC पर BD लम्ब डाले
प्रमाण:- त्रिभुज ADB तथा ABC में,
∠ADB = ∠ABC = 90°
∠DAB = ∠BAC (उभयनिष्ठ कोण)
AA समरूपता कसौटी से,
ΔADB~ΔABC
∴
...(1)
इसी प्रकार त्रिभुज CDB तथा CBA में
∠CDB = ∠ABC = 90°
∠BCD = ∠ACB (उभयनिष्ठ कोण)
AA समरूपता कसौटी से,
ΔCDB~ΔCBA
∴
...(2)
समीकरण (1) + समीकरण (2)
∴ }
Q21. Prove that in a triangle, if square of one side is equal to the sum of the squares of the other two sides then the angle opposite the first side is a right angle.
{सिद्ध कीजिए कि यदि किसी त्रिभुज की एक भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर हो तो पहली भुजा का सम्मुख कोण समकोण होता है|}
Ans. Given:- ΔABC in which
Prove:- ∠B=90°
Construction:- Draw a ΔXYZ right angled at Y, such that AB=XY and BC=YZ.
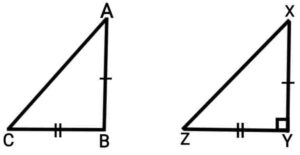 Proof:- In ΔXYZ
Proof:- In ΔXYZ
(By Pythagoras theorem)
or
(By construction)
But given
From equation(i) and equation(ii),
AC=XZ
Now, in ΔABC and ΔXYZ,
AB=XY
BC=YZ
AC=XZ
By SSS congruency criterion,
ΔABC≅ΔXYZ
By CPCT,
∠B=∠Y
But ∠Y=90°
∠B=90°.
{दिया है:- ΔABC जिसमें
सिद्ध करना है:- ∠B=90°
रचना:- एक ΔXYZ खींचिए जो Y पर समकोण हो, जिससे AB=XY और BC=YZ हो|
 प्रमाण:- ΔXYZ में
प्रमाण:- ΔXYZ में
(पाइथागोरस प्रमेय द्वारा)
या
(निर्माण द्वारा)
लेकिन दिया हुआ है
समीकरण(i) और समीकरण(ii) से,
AC=XZ
अब, ΔABC और ΔXYZ में,
AB=XY
BC=YZ
AC=XZ
SSS सर्वांगसमता कसौटी से,
ΔABC≅ΔXYZ
CPCT द्वारा,
∠B=∠Y
लेकिन Y=90°
B=90°}
Q22. Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
{सिद्ध कीजिए कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है|}
Ans. Given:- 2 triangles such that
ΔABC∼ΔPQR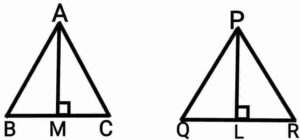 Prove:-
Prove:-
Construction:- Draw AM⊥BC and PL⊥QR
Proof:-
Now, equation(i) equation(ii)
Now, in ΔABM and ΔPQL
∠B=∠Q (ΔABC∼ΔPQR)
∠AMB=∠PLQ=90°
By AA similarity criterion,
ΔABM∼ΔPQL
And given ΔABC∼ΔPQR
Now, putting the value of equation(v) that in equation(iii)
i.e.
Now, putting the value of equation(iv) in equation(vi)
i.e.
Now, using equation(v)
{दिया हुआ है:- 2 त्रिभुज इस प्रकार हैं कि
ΔABC∼ΔPQR सिद्ध करना है:-
सिद्ध करना है:-
रचना:- AM⊥BC और PL⊥QR बनाए
प्रमाण:-
अब, समीकरण(i) समीकरण(ii)
अब, ΔABM और ΔPQL में,
∠B=∠Q (ΔABC∼ΔPQR)
∠AMB=∠PLQ=90°
AAA समरूपता कसौटी से,
ΔABM∼ΔPQL
और दिया हुआ है ΔABC∼ΔPQR
अब, समीकरण(v) का मान को समीकरण (iii) में रखने पर
अर्थात्
अब, समीकरण(iv) का मान समीकरण (vi) में रखने पर
अर्थात्
अब, समीकरण(v) का उपयोग करने पर
}
9113323460

I hope you like it. If you like then please share it and you can also Donate to our website by my number and QR code which is given above.
Thanks.
