Some applications of trigonometry (त्रिकोणमिति के कुछ अनुप्रयोग)
Get “Some applications of trigonometry” chapter’s previous years questions from 2009 to 2020 of JAC board.
Q1. From the top of a 7m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
{7m ऊंँचे भवन के शिखर से एक केबल टावर के शिखर का उन्नयन कोण 60° है और इसके पाद का अवनमन कोण 45° है| टावर की ऊंँचाई ज्ञात कीजिए|}
Ans.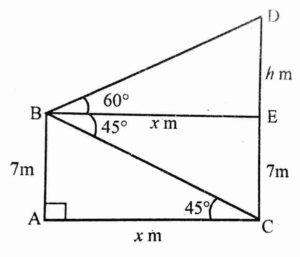 In the figure,
In the figure,
AB(=7) is the building,
CD{=(h+7)} is the tower and
AC(=x) is the distance of building and tower.
Now, In ΔDEB,
…(1)
And in ΔBAC,
putting the value of x in equation (1)
∴ Height of tower CD=DE+CE=h+7
{
आकृति में,
AB(=7) भवन है,
CD{=(h+7)} टावर है और
AC(=x) भवन और टावर की दूरी है।
अब, ΔDEB में,
…(1)
और ΔBAC में,
x का मान समीकरण(1) में रखने पर
टावर CD की ऊंँचाई=DE+CE=h+7
}
Q2. The shadow of a tower standing on a level ground is found to be 40m longer when the sun’s altitude is 30° than when it is 60°. Find the height of the tower.
{एक समतल जमीन पर खड़ी मीनार की छाया उस स्थिति में 40m अधिक लंबी हो जाती है जबकि सूर्य का उन्नतांश 60° से घटकर 30° हो जाता है|मीनार की ऊंचाई ज्ञात कीजिए}
Ans.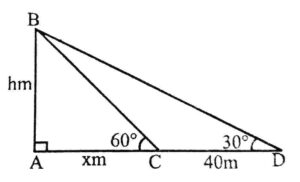 In the figure,
In the figure,
AB(=h) is the tower,
AC(=x) is length of shadow when sun’s altitude is 60° and
AD{=(x+40)} is length of shadow when sun’s altitude is 30°
In ΔABC,
And in ΔBAD,
Now, putting the value of x
m
∴ height of the tower=
{ आकृति में,
आकृति में,
AB(=h) मीनार है,
AC(=x) छाया की लंबाई है जब सूर्य की ऊंचाई 60° होती हैं और
AD{=(x+40)} छाया की लंबाई है जब सूर्य की ऊंचाई 30° होती हैं|
ΔABC मे,
और ΔBAD मे ,
x का मान रखने पर
∴ मीनार की ऊंचाई= }
Q3. The shadow of a tower standing on a level ground is found to be 40m longer when the sun’s altitude is 30° then when it is 60°.
(a) Draw a simple diagram(figure) to demonstrate the question.
(b) Write the name of the right angled triangle formed in the simple.
(c) Find out the height of the tower.
{एक समतल जमीन पर खड़ी मीनार की छाया उस स्थिति में 40m अधिक लंबी हो जाती है जबकि सूर्य का उन्नतांश 60° से घटकर 30° हो जाता है|
(a) प्रशनों को निरूपित करने के लिए एक सरल आरेख(चित्र) बनाइये|
(b) सरल आरेख में बने कोण त्रिभुज का नाम लिखिए|
(c) मीनार की ऊंचाई ज्ञात कीजिए}
Ans.(a) (b) ΔABC and ΔBAD are right angled triangles.
(b) ΔABC and ΔBAD are right angled triangles.
(c)In the figure,
AB(=h) is the tower,
AC(=x) is length of shadow when sun’s altitude is 60° and
AD{=(x+40)} is length of shadow when sun’s altitude is 30°
In ΔABC,
And in ΔBAD,
Putting the value of x
m
∴ height of the tower=
{(a) (b) ΔABC और ΔBAD समकोण त्रिभुज है|
(b) ΔABC और ΔBAD समकोण त्रिभुज है|
(c)आकृति में,
AB(=h) मीनार है,
AC(=x) छाया की लंबाई है जब सूर्य की ऊंचाई 60° होती हैं और
AD{=(x+40)} छाया की लंबाई है जब सूर्य की ऊंचाई 30° होती हैं
ΔABC मे,
…(1)
और ΔBAD मे ,
x का मान रखने पर
∴ मीनार की ऊंचाई= }
Q4. Two poles of equal heights are standing opposite to each other on either side of the road, which is 80m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30° respectively. Find the height of the poles and distances of the point from the poles.
{एक 80m चौड़ी सड़क के दोनों ओर आमने-सामने समान लंबाई वाले दो खंभे लगे हुए हैं| उन दोनों खंभों के बीच सड़क के एक बिंदु से खंभों के शिखर के उन्नयन कोण क्रमशः 60° और 30° है| खंभों की उचाई और खंभों से बिंदु की दूरी ज्ञात कीजिए|}
Ans.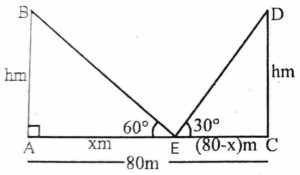 In the figure,
In the figure,
AB(=h) and CD(=h
) are the 2 equal poles,
AC(=80) is wide road and
E is a point between the 2 poles on the road.
In ΔBAE,
…(1)
And in ΔDCE,
Putting the value of h
putting the value of x in equation (1)
∴ Height(h) of the pole=,
Distance(x) of the point from the 1st pole=20m and
Distance of the point from the 2nd pole=(80-x) =80-20 =60m.
{ आकृति में,
आकृति में,
AB(=h) और CD(=h
) दो समान खंभे हैं,
AC(=80) चौड़ी सड़क है और
E सड़क पर दो खंभे के बीच का एक बिंदु है।
ΔBAE मे,
…(1)
और ΔDCE मे ,
h का मान रखने पर
x का मान समीकरण (1) मे रखने पर
∴ खंभों की उचाई(h) =,
पहले खम्भा से बिंदु की दूरी(x)=20 और
दूसरे खम्भा से बिंदु की दूरी=(80-x) =80-20 =60}
Q5. A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8m. Find the height of the tree.
{आंँधी आने से एक पेड़ टूट जाता है और टूटा हुआ भाग इस तरह मुड़ जाता है कि पेड़ का शिखर जमीन को छूने लगता है और उसके साथ 30° का कोण बनाता है| पेड़ के पाद-बिंदु की दूरी जहाँ पेड़ का शिखर जमीन को छूता है,8m है| पेड़ की ऊंँचाई ज्ञात कीजिए|
Ans.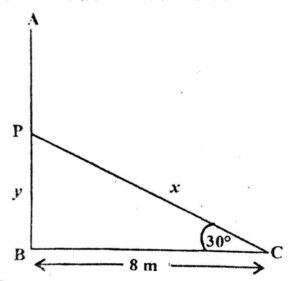
In the figure,
AB(=h) is a tree,
PC=AP(=x) is the broken part,
BC(=8) is the distance between the foot of the tree to the point where the top touches the ground and
∠PCB=30°
In ΔPBC,
and
∴ Height of tree=AP+PB=x+y
{
आकृति में,
AB(=h) एक पेड़ है,
PC=AP(=x) टूटा हुआ हिस्सा है,
BC(=8) पेड़ के पाद से बिंदु की दूरी है (जहाँ पेड़ का शिखर जमीन को छूता है) और
∠PCB=30°
ΔPBC में,
और
∴ पेड़ की ऊंँचाई=AP+PB=x+y
}
Q6. From a point on a bridge across a river, the angles of depression of the banks on opposite of the river are 30° and 45° respectively. If the bridge is at a height of 3m from the banks, find the width of the river.
{एक नदी के पुल के एक बिंदु से नदी के सम्मुख किनारों के अवनमन कोण क्रमशः 30° और 45° हैं| यदि पुल किनारे से 3m की ऊँचाई पर हो, तो नदी की चौड़ाई ज्ञात कीजिये|}
Ans.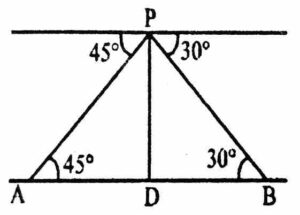 In the figure,
In the figure,
AB is the width of river
and P is a point on the bridge which is 3m above the river.
In ΔPDA,
And in ΔPDB,
∴ Width of river AB=AD+DB
{ आकृति में,
आकृति में,
AB नदी की चौड़ाई है
और P पुल पर एक बिंदु है जो नदी से 3 मीटर ऊपर है।
ΔPDA मे ,
और ΔPDB मे,
∴ नदी AB की चौड़ाई =AD+DB
}
Q7. From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20m high building are 45° and 60° respectively. Find the height of the tower.
{भूमि के एक बिंदु से 20m ऊँचे भवन के शिखर पर लगी संचार मीनार के तल और शिखर के उन्नयन कोण का क्रमशः 45° और 60° हैं| मीनार की ऊँचाई ज्ञात कीजिये|
Ans.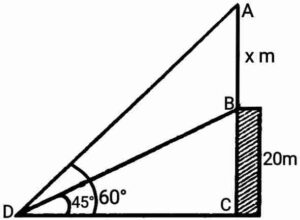 In the figure,
In the figure,
BC(=20m) is a building and
AB(=x) is a tower
In ΔBDC,
And in ΔADC,
{
आकृति में,
BC(=20m) एक भवन है और
AB एक मीनार है
ΔBDC मे,
और ΔADC मे,
मीनार की ऊँचाई
}
Q8. The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of a tower from the foot of the building is 60°. If the tower is 50m high, find the height of the building.
{एक मीनार का पाद-बिंदु से एक भवन के शिखर का उन्नयन कोण 30° है और भवन के पाद-बिंदु से मीनार के शिखर का उन्नयन कोण 60° है| यदि मीनार 50 मीटर ऊँची है, तो भवन की ऊँचाई ज्ञात कीजिए।}
Ans.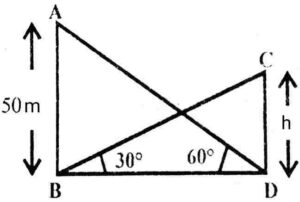 In the figure,
In the figure,
AB(=50) is a tower and
CD(=h) is a building
Now in ΔABD,
and in ΔCDB,
Putting the value of BD
∴ The height of the building
{ आकृति में,
आकृति में,
AB(=50) एक मीनार है और
CD(=h) एक भवन है
अब ΔABD में,
और ΔCDB में,
BD का मान रखने पर
∴ अतः भवन की ऊँचाई है }
Q9. From a point P on the ground, the angle of elevation of the top of the 10m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flagstaff from P is 45°, find the length of the flagstaff. (take )
{भूमि के एक बिंदु P से एक 10m ऊँचे भवन के शिखर का उन्नयन कोण 30° है| भवन के शिखर से एक ध्वज को लहराया गया है और P से ध्वज के शिखर का उन्नयन कोण 45° है| ध्वजदंड की लम्बाई ज्ञात कीजिये| ( लीजिये )}
Ans. 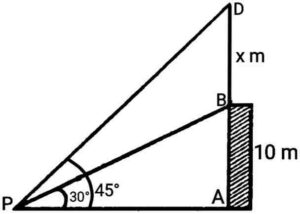 In the figure,
In the figure,
AB(=10) is a building and
DB(=x) is a flag
In ΔBPA,
and ΔDPA,
∴ the length of the flagstaff
{ आकृति में,
आकृति में,
AB(=10) एक भवन है और
DB(=x) एक झंडा है
अब ΔBPA में,
और ΔDPA में,
∴ ध्वजदंड की लम्बाई }
Q10. A worker 1.5m tall is 28.5m away from a chimney of furnace. The angle of elevation of the top of the chimney from his eye is 45°. What is the height of the chimney?
{1.5m लम्बा एक प्रेक्षक एक चिमनी से 28.5m की दूरी पर स्थित है| उसकी आँखों से चिमनी के शिखर का उन्नयन कोण 45° है| चिमनी की ऊँचाई ज्ञात कीजिये|}
Ans.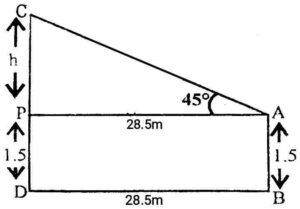 In the figure,
In the figure,
AB(=1.5) is a worker,
CD{=(h+1.5)} is the chimney and
DB=PA(=28.5) is the distance of chimney to worker.
Now in ΔCPA,
CP=h , ∠CAP=45°
Now,
AB=PD=1.5
∴ CD=CP+PD=h+1.5
=28.5+1.5=30
{ आकृति में,
आकृति में,
AB(=1.5) एक प्रेक्षक है,
CD{=(h+1.5)} चिमनी है और
DB=PA(=28.5) चिमनी से प्रेक्षक की दूरी है।
अब ΔCPA में,
CP=h , ∠CAP=45°
अब, AB=PD=1.5
∴ CD=CP+PD=h+1.5
=28.5+1.5=30}
Q11. The angles of elevation of the top of a tower from two points at a distance of 4m and 9m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6m.
{मीनार के आधार से और एक ही सरल रेखा में 4m और 9m की दूरी पर स्थित दो बिंदुओं से मीनार के शिखर के उन्नयन कोण पूरक कोण हैं| सिद्ध कीजिए कि मीनार की ऊँचाई 6m है|}
Ans. 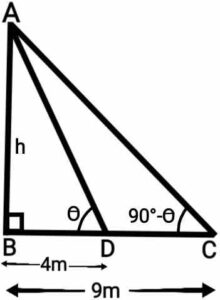 In the figure,
In the figure,
AB(=h) is the tower,
BD=4m, BC=9m,
and
In right ΔABD,
Now, in right ΔABC
From equation(i)
Height of the tower is 6m.
{ आकृति में,
आकृति में,
AB(=h) मीनार है,
BD=4m, BC=9m,
और
समकोण ΔABD में,
अब, समकोण ΔABC में,
समीकरण(i) से,
मीनार की ऊँचाई 6m है|}
9113323460

I hope you like it. If you like then please share it and you can also Donate to our website by my number and QR code which is given above.
Thanks.
