Circles (वृत्त)
Get “Circles” chapter’s previous years questions from 2009 to 2020 of JAC board.
Q1. How many parallel tangents are possible for a circle?
{एक वृत्त की कितनी समांतर स्पर्श रेखाएं हो सकती है?}
Ans. 2
Q2. What is called a line intersecting a circle in two points?
{वृत्त को दो बिंदुओं पर प्रतिच्छेद करने वाली रेखा को क्या कहते हैं?}
Ans. Secant line
{छेदक रेखा}
Q3. How many tangents can a circle have?
{एक वृत्त की कितनी स्पर्श रेखाएं होती है?}
Ans. Infinite
{अनेक स्पर्श रेखाएं हो सकती है}
Q4. Fill in the blank:
The common point of a tangent to a circle and the circle is called…
{रिक्त स्थान की पूर्ति कीजिए:
वृत्ते तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिंदु को…कहते हैं।}
Ans. Point of contact
{स्पर्श बिंदु}
Q5. A tangent PQ at a point P of a circle with the radius 7cm meets a line through the centre O at a point Q so that OQ=13cm. What is the length of PQ?
{7cm त्रिज्या वाले एक वृत्त के बिंदु P पर स्पर्श रेखा PQ केंद्र O से जाने वाली एक रेखा से बिंदु Q पर इस प्रकार मिलती है कि OQ=13cm| PQ की लंबाई लिखिए|}
Ans.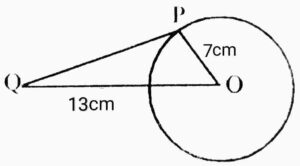
Appling Pythagoras theorem,
{
पाइथागोरस प्रमेय से,
}
Q6. In the figure, a tangent PQ at a point P of a circle with the radius 5cm meets a line through the centre O at a point Q so that OQ=11cm, what is the length of PQ?
{चित्र में, 5cm त्रिज्या वाले एक वृत्त के बिंदु P पर स्पर्श रेखा PQ केंद्र O से जाने वाली एक रेखा से बिंदु Q पर इस प्रकार मिलती है कि OQ=11cm, PQ की लंबाई लिखिए|}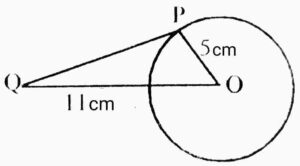
Ans. Appling Pythagoras theorem,
{पाइथागोरस प्रमेय से,
}
Q7. In the given figure, tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°. Then ∠POA is equal to
{दिए गए आकृति में, यदि एक बिंदु P से O केंद्र वाले किसी वृत्त पर PA और PB स्पर्श रेखाएं परस्पर 80° के कोण पर झुकी हो, तो ∠POA ज्ञात कीजिए}
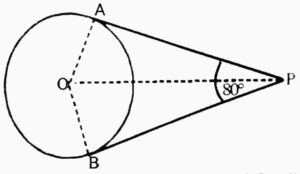
Ans. Here, OP bisect the angle between the two tangents.
In ΔOAP,
∠POA+∠OAP+∠APO=180°
∠POA+90°+40°=180°
∠POA=180°-130°=50°
{यहाँ, OP दो स्पर्श रेखाओं के बीच के कोण को समद्विभाजित कर रहा हैं।
ΔOAP में ,
∠POA+∠OAP+∠APO=180°
∠POA+90°+40°=180°
∠POA=180°-130°=50°}
Q8. In the given figure, if TP and TQ are two tangents to a circle with centre O, so that ∠POQ=110°,then find ∠PTQ
{दिए गए आकृति में, यदि TP तथा TQ केंद्र O वाले किसी वृत्त पर दो स्पर्श रेखाएं इस प्रकार है कि ∠POQ=110°, तो ∠PTQ का मान लिखिए}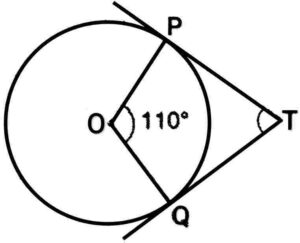
Ans. In quadrilateral OPTQ
∠QOP+∠OPT+∠PTQ+∠TQO=360°
110°+90°+∠PTQ+90°=360°
∠PTQ=360°-290°=70°
∴ ∠PTQ=70°
{चतुर्भुज OPTQ मे,
∠QOP+∠OPT+∠PTQ+∠TQO=360°
110°+90°+∠PTQ+90°=360°
∠PTQ=360°-290°=70°
∴ ∠PTQ=70°}
Q9. A quadrilateral ABCD is drawn to circumscribing a circle. Prove that AB+CD=AD+BC.
{एक वृत्त के परिगत एक चतुर्भुज ABCD खींचा गया है|सिद्ध कीजिए कि AB+CD=AD+BC}
Ans.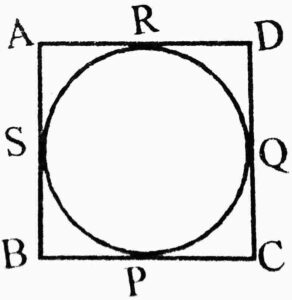
Let ABCD is a quadrilateral, which touches the circle at points P,Q,R and S respectively.
The lengths of tangents drawn from an exterior point to a circle are equal.
AS=AR, SB=BP, CQ=PC and QD=RD
Now, AB+CD=(AS+SB)+(CQ+QD)
AB+CD=(AR+BP)+(PC+RD)
After rearranging,
AB+CD=(AR+RD)+(BP+PC)
AB+CD=AD+BC
AB+CD=AD+BC
{माना की ABCD एक चतुर्भुज है जो एक वृत्त को क्रमशः P,Q,R और S बिन्दुओ पर छूता है
बाह्य बिंदु से वृत्त पर खींची गई स्पर्श रेखाएँ की लम्बाई समान होती है
AS=AR, SB=BP, CQ=PC and QD=RD
Now, AB+CD=(AS+SB)+(CQ+QD)
AB+CD=(AR+BP)+(PC+RD)
पुनर्व्यवस्थित करने के बाद,
AB+CD=(AR+RD)+(BP+PC)
AB+CD=AD+BC
AB+CD=AD+BC}
Q10. Prove that the lengths of the tangents drawn from an external point to a circle are equal.
{सिद्ध कीजिए कि बाह्य बिंदु से वृत्त पर खींची गई स्पर्श रेखाओं की लंबाई बराबर होती है}
Ans.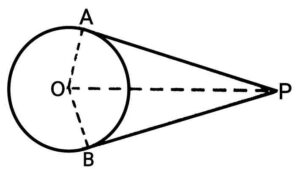
Let a circle whose centre is O and two tangent PA and PB is drawn from the external point P.
Prove : PA=PB
Construction : Join OA,OB and OP
Proof : In ΔOAP and ΔOBP
∠OAP=∠OBP=90° (Radius⊥tangent)
OP=OP (common)
OA=OB (radii)
By RHS congruency criterion,
ΔOAP≅ΔOBP
∴ By CPCT
PA=PB
{माना कि एक वृत्त जिसका केंद्र O है और दो स्पर्श रेखाएँ PA और PB बाहरी बिंदु P से खींची गई हैं।
सिद्ध करना है : PA=PB
रचना : OA,OB तथा OP को मिलाया
प्रमाण : ΔOAP और ΔOBP में ,
∠OAP=∠OBP=90° (त्रिज्या⊥स्पर्श रेखा)
OP=OP (उभयनिष्ठ)
OA=OB (त्रिज्या)
RHS सर्वांगसमता कसौटी से ,
ΔOAP≅ΔOBP
∴ CPCT से,
PA=PB}
Q11. Prove that the tangents drawn at the ends of the diameter of a circle are parallel.
{सिद्ध कीजिए कि किसी वृत्त के किसी व्यास के सिरों पर खींचे गए स्पर्श रेखाएं समांतर होती है।}
Ans.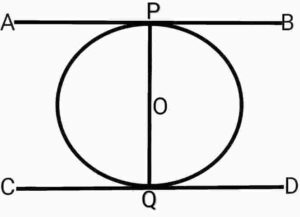
Let a circle with centre O and PQ is a diameter.
and, AB and CD is tangents which touches the circle at P and Q.
Prove : AB||CD
Proof : PQ is diameter, then OP and OQ is radius.
And we know that, Radius of circle ⊥ tangent of circle.
∴ OP⊥AB and OQ⊥CD
∴ ∠APQ=∠DQP=90°
and ∠BPQ=∠CQP=90°
Here, (∠APQ and ∠DQP) and (∠BPQ and ∠CQP) makes alternate interior angles.
So, it can be said that lines AB and CD will be parallel to each other.
∴ AB||CD
{माना की एक वृत्त जिसका केंद्र O है तथा PQ एक व्यास है|
और, AB और CD स्पर्श रेखाएँ हैं जो वृत्त को P और Q पर स्पर्श करती हैं।
सिद्ध करना है : AB||CD
प्रमाण : PQ व्यास है, तो OP और OQ त्रिज्या होगा|
और हम जानते हैं कि, वृत्त की त्रिज्या ⊥ स्पर्श रेखा|
∴ OP⊥AB and OQ⊥CD
∴ ∠APQ=∠DQP=90°
and ∠BPQ=∠CQP=90°
यहाँ , (∠APQ और ∠DQP) और (∠BPQ और ∠CQP) एकांतर आंतरिक कोण बना रहा है|
तो, यह कहा जा सकता है कि रेखाएं AB और CD एक दूसरे के समानांतर होंगी|
∴ AB||CD }
Q12. Prove that in two concentric circles, the chord of the larger circle, which touches the smaller circle ,is bisected at the point of contact.
{सिद्ध कीजिए कि दो संकेंद्रीय वृत्तों में बड़े वृत्त की जीवा जो छोटे वृत्त को स्पर्श करती है, स्पर्श बिंदु पर सम-द्विभाजित होती है}
Ans.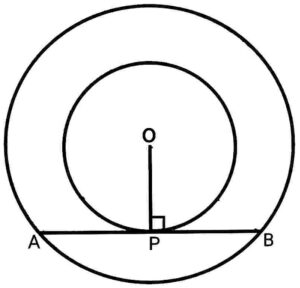
Given : 2 concentric circles with common centre O and a chord AB of the larger circle which touches the smaller circle at the point P.
Prove: AP=BP
Construction: Join OP
Proof: Radius of small circle ⊥ tangent of small circle.
∴ OP⊥AB
Now, AB is a chord of the big circle and OP⊥AB.
As we know that the perpendicular from the centre of circle bisect the chord.
i.e, OP is the perpendicular from the centre of big circle which bisect the chord AB.
∴ AP=BP
{
दिया है : उभयनिष्ठ केंद्र O वाले 2 संकेंद्रित वृत्तों और बड़े वृत्त की एक जीवा AB जो छोटे वृत्त को बिंदु P पर स्पर्श करती है।
सिद्ध करना है : AP=BP
रचना : OP को मिलाया
प्रमाण : छोटे वृत्त की त्रिज्या ⊥ छोटे वृत्त की स्पर्श रेखा
∴ OP⊥AB
अब, AB बड़े वृत्त की जीवा है और OP⊥AB
जैसा कि हम जानते हैं कि वृत्त के केंद्र से लम्ब जीवा को समद्विभाजित करता है।
अर्थात् OP बड़े वृत्त के केंद्र से लम्ब है जो जीवा AB को समद्विभाजित करता है।
∴ AP=BP}
Q13. Prove that the parallelogram circumscribing a circle is a rhombus.
{सिद्ध कीजिए कि किसी वृत्त के परिगत समांतर चतुर्भुज एक समचतुर्भुज होता|}
Ans.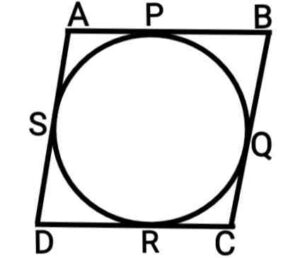 
Given:- ABCD is a parallelogram in which AB=CD and BC=DA
Prove:- AB=BC=CD=DA
Proof:- The lengths of tangents drawn from an exterior point to a circle are equal.
AP=SA, PB=BQ, CR=QC and RD=DS
Adding all
AP+PB+CR+RD=SA+BQ+QC+DS
AB+CD=DA+BC
AB+AB=BC+BC
( AB=CD and BC=DA)
2AB=2BC
AB=BC
AB=BC
AB=CD and BC=DA
That means, AB=BC=CD=DA
Hence, ABCD is the parallelogram.
{दिया हुआ है:- ABCD एक समांतर चतुर्भुज है जिसमें AB=CD और BC=DA
सिद्ध करना है:- AB=BC=CD=DA
प्रमाण:- बाह्य बिंदु से वृत्त पर खींची गई स्पर्श रेखाएँ की लम्बाई समान होती है
AP=SA, PB=BQ, CR=QC और RD=DS
सभी को जोड़ना पर
AP+PB+CR+RD=SA+BQ+QC+DS
AB+CD=DA+BC
AB+AB=BC+BC
( AB=CD और BC=DA)
2AB=2BC
AB=BC
AB=BC
AB=CD और BC=DA
इसका अर्थ है, AB=BC=CD=DA
अत: ABCD समांतर चतुर्भुज है|}
9113323460
I hope you like it. If you like then please share it and you can also Donate to our website by my number and QR code which is given above.
Thanks.