Areas related to circles (वृत्तों से संबंधित क्षेत्रफल)
Get “Areas related to circles” chapter’s previous years questions from 2009 to 2020 of JAC board.
Q1. Write the area of a semicircle of radius r.
{r त्रिज्या वाले अर्धवृत्त का क्षेत्रफल लिखिए}
Ans. Area of semicircle
{अर्धवृत्त का क्षेत्रफल }
Q2. Write the area of a semicircle of radius r=7cm.
{r=7cm त्रिज्या वाले अर्धवृत्त की क्षेत्रफल लिखिए}
Ans. Area of semicircle
{अर्धवृत्त की क्षेत्रफल }
Q3. Write the area of a semicircle of radius r=14cm.
{ r=14cm त्रिज्या वाले अर्धवृत्त की क्षेत्रफल लिखिए}
Ans. Area of semicircle
{अर्धवृत्त की क्षेत्रफल}
Q4. Write the area of a circle of radius r
{ r त्रिज्या वाले वृत्त का क्षेत्रफल लिखिए}
Ans. Area of circle
{वृत्त का क्षेत्रफल }
Q5. Write the perimeter of a circle of diameter d.
{व्यास d वाले वृत्त का परिमाप लिखिए}
Ans. Perimeter of a circle =πd
{वृत्त का परिमाप =πd}
Q6. Write the perimeter of a circle of radius r.
{r त्रिज्या वाले वृत्त का परिमाप लिखिए}
Ans. Perimeter of a circle =2πr
{वृत्त का परिमाप =2πr}
Q7. Write the perimeter of a semicircle of radius r.
{r त्रिज्या वाले अर्धवृत्त का परिमाप लिखिए}
Ans. Perimeter of a semicircle
{अर्धवृत्त का परिमाप
या
}
Q8. If the perimeter of semicircle is 36cm, then find its diameter.
{यदि एक अर्धवृत्त का परिमाप 36cm है, तो उसका व्यास ज्ञात कीजिए}
Ans.
Q9. If the perimeter and the area of circle are numerically equal, then write the radius of the circle.
{यदि एक वृत्त के परिमाप और क्षेत्रफल संख्यात्मक रूप से बराबर है तो वृत्त का त्रिज्या लिखिए}
Ans. Perimeter of circle =area of circle
{वृत्त के परिमाप =वृत्त के क्षेत्रफल
}
Q10. Find the area of quadrant of a circle whose circumference is 22cm.
{एक वृत्त के चतुर्थांश का क्षेत्रफल ज्ञात कीजिए, जिसकी परिधि 22cm है}
Ans. 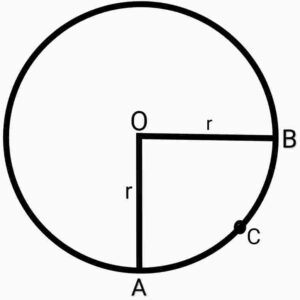 Given:- Circumference of circle =22cm
Given:- Circumference of circle =22cm
∴ Area of quadrant OACB
{ दिया हुआ है:- वृत्त के परिधि =22cm
दिया हुआ है:- वृत्त के परिधि =22cm
∴ चतुर्थांश OACB का क्षेत्रफल }
Q11. Find the area of sector of a circle with radius 6cm if angle of the sector is 60°.
{6cm त्रिज्या वाले एक वृत्त के एक त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए जिसका कोण 60° है}
Ans. 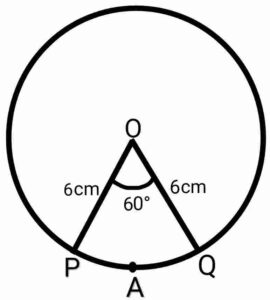 Given:- r= 6cm and θ=60°
Given:- r= 6cm and θ=60°
∴ Area of sector OPAQ
{ दिया हुआ है:- r= 6cm और θ=60°
दिया हुआ है:- r= 6cm और θ=60°
∴ त्रिज्यखंड OPAQ का क्षेत्रफल
}
Q12. In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find (a) the length of arc, (b) area of the sector formed by the arc.
{त्रिज्या 21cm वाले वृत्त का एक चाप केंद्र पर 60° का कोण अंतरित करता है। ज्ञात कीजिए (a) चाप की लंबाई (b) चाप द्वारा बनाए गए त्रिज्यखंड का क्षेत्रफल}
Ans. 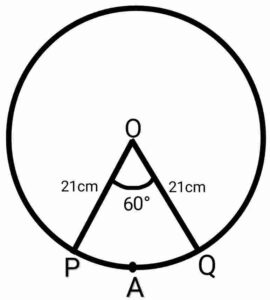
Given:- r= 21cm and θ=60°
(a) the length of arc PQ
(b) area of the sector OPAQ formed by the arc PQ
{ दिया हुआ है:- r= 21cm और θ=60°
दिया हुआ है:- r= 21cm और θ=60°
(a) चाप PQ की लंबाई
(b) चाप PQ द्वारा बनाए गए त्रिज्यखंड OPAQ का क्षेत्रफल }
Q13. A chord of a circle of radius 10cm subtends a right angle at the centre of the circle. Find out the area of corresponding minor sector of circle.
{ 10cm त्रिज्या वाले एक वृत्त का कोई जीवा केंद्र पर एक समकोण अंतरित करती है। संगत लघु त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए}
Ans.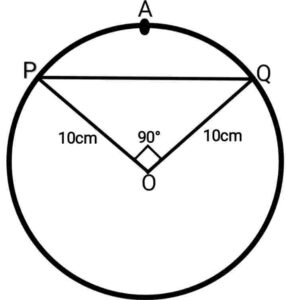 Given:- r=10cm and θ=90°
Given:- r=10cm and θ=90°
∴ Area of minor sector of circle OPAQ
{ दिया हुआ है:- r=10cm and θ=90°
दिया हुआ है:- r=10cm and θ=90°
∴ लघु त्रिज्यखंड OPAQ का क्षेत्रफल }
Q14. Find out the area of the sector of a circle having radius 4cm and of angle 30°. Also, find out the area of the corresponding major sector
{त्रिज्या 4cm वाले एक त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण 30° है| साथ ही संगत दीर्घ त्रिज्यखंड का क्षेत्रफल भी ज्ञात कीजिए।
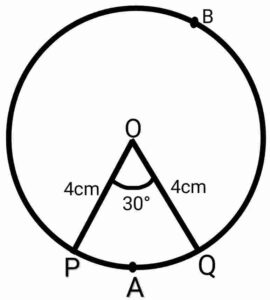
Ans.Given:- r=4cm and θ=30°
Area of the minor sector OPAQ
∴ The area of the major sector OPBQ = area of circle – area of minor sector OPAQ
{ दिया हुआ है:- r=4cm and θ=30°
दिया हुआ है:- r=4cm and θ=30°
लघु त्रिज्यखंड OPAQ का क्षेत्रफल
∴ दीर्घ त्रिज्यखंड OPBQ का क्षेत्रफल = वृत्त का क्षेत्रफल – लघु त्रिज्यखंड OPAQ का क्षेत्रफल
}
Q15. The length of the minute hand of a clock is equal to 14cm. Find out the area swept by the minute hand in 5 minutes.
{एक घड़ी की मिनट की सुई की लंबाई 14cm है। उसके द्वारा 5 मिनट में रचित क्षेत्रफल ज्ञात कीजिए}
Ans. Angle formed in 60 minutes =360°
So, angle formed in 5 minutes
Here, radius of circle =length of the minute hand of a clock =14cm
∴ The area swept by the minute hand in 5 minutes
{60 मिनट में बना केंद्रीय कोण =360°
तो 5 मिनट में बना केंद्रीय कोण
चूँकि वृत्त की त्रिज्या =घड़ी की सुई की लम्बाई =14cm
∴ 5 मिनट में सुई द्वारा रचित क्षेत्रफल
}
Q16. A chord of a circle of radius 15cm subtends an angle of 60° at the centre of the circle. Find out the area of the corresponding minor segment of the circle.(using π=3.14 and )
{15cm त्रिज्या वाले एक वृत्त को कोई जीवा केंद्र पर 60° का कोण अंतरित करती है। संगत लघु वृत्तखंड का क्षेत्रफल ज्ञात कीजिए}
( π=3.14 और का प्रयोग कीजिए}
Ans.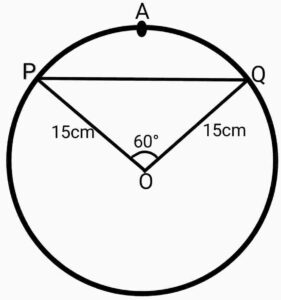 Area of sector OPAQ
Area of sector OPAQ
Now, in ΔOPQ, draw OL⊥PQ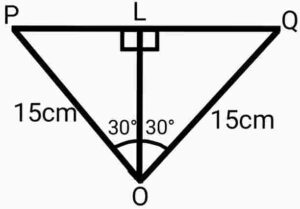 Now, OP=OQ (radii)
Now, OP=OQ (radii)
OL=OL (common)
∠OLP=∠OLQ=90°
∴ By R.H.S criterion
ΔOLP≅ΔOLQ
By, CPCT
PL=LQ
and ∠POL=∠QOL
In ΔPOL,
PL=LQ
PQ=2×PL= =15cm
Now, In ΔPOL,
∴ area of ΔOPQ
Area of minor segment PAQ = Area of sector OPAQ – Area of ΔOPQ
{
त्रिज्यखंड OPAQ का क्षेत्रफल
अब, ΔOPQ में, OL⊥PQ खीचिए अब, OP=OQ (त्रिज्या)
अब, OP=OQ (त्रिज्या)
OL=OL (उभयनिष्ठ)
∠OLP=∠OLQ=90°
∴ R.H.S कसौटी से,
ΔOLP≅ΔOLQ
CPCT से,
PL=LQ
और ∠POL=∠QOL
ΔPOL में,
PL=LQ
PQ=2×PL= =15cm
अब, ΔPOL में,
∴ ΔOPQ का क्षेत्रफल
लघु वृत्तखंड PAQ का क्षेत्रफल = त्रिज्यखंड OPAQ का क्षेत्रफल – ΔOPQ का क्षेत्रफल
}
Q17. The wheels of a car are of diameter 80cm each. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at the speed of 66 km/hour?
{किसी कार के प्रत्येक पहिया का व्यास 80cm है। यदि यह कार 66किमी.प्रति घंटे की चाल से चल रही है तो 10 मिनट में प्रत्येक पहिया कितने चक्कर लगाती है?}
Ans. The diameter of each wheels of a car =80cm
So, radius(r)
Now, The car is travelling at the speed of 66 km/hour
means,
∴ distance travelled by car in 10 minutes =110000×10 =1100000cm
Now, the circumference of wheel
So, revolutions does each wheel make in 10 minutes
∴ Revolutions does each wheel make in 10 minutes =4375
{चूँकि कार के प्रत्येक पहिए का व्यास d=80cm है
तब इसकी त्रिज्या
अब, कार 66किमी.प्रति घंटे की चाल से चल रही है
अर्थात,
∴ 10 मिनट में कार द्वारा तय की गई दुरी =110000×10 =1100000cm
अब, पहिए का परिधि
तो 10 मिनट में प्रत्येक पहिया चक्कर लगाती है =10 मिनट में कार द्वारा तय की गई दुरी ÷ पहिए का परिधि
∴ 10 मिनट में प्रत्येक पहिया चक्कर लगाती है =4375}
Q18. Find the area of the shaded region in figure, where ABCD is a square of side 14cm.
{आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, जहाँ ABCD भुजा 14cm का एक वर्ग है|}
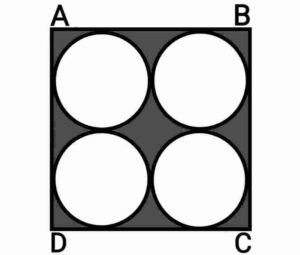
Ans. Side of square ABCD=14cm.
So, diameter of each circle
Radius(r) of each circle
Now, area of shaded region
area of square ABCD
(4×area of a circle)
Area of the shaded region
{वर्ग ABCD की भुजा=14cm
तो, प्रत्येक वृत्त का व्यास
प्रत्येक वृत्त की त्रिज्या(r)
अब, छायांकित भाग का क्षेत्रफल
वर्ग ABCD का क्षेत्रफल
(4×एक वृत्त का क्षेत्रफल)
छायांकित भाग का क्षेत्रफल
}
Q19. Find the area of the shaded region in figure, if the radii of the two concentric circles with centre O are 7cm and 14cm respectively and ∠AOC=40°.
{आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए यदि केंद्र O वाले दोनों संकेंद्रित वृत्तों की त्रिज्याएँ क्रमशः 7cm और 14cm हैं तथा ∠AOC=40° हैं|}
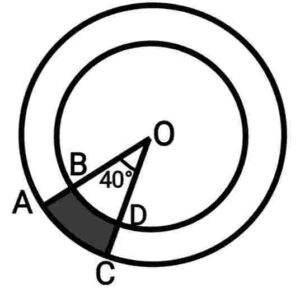
Ans. Let OB=r=7cm
and OA=R=14cm
Now, area of the shaded region
area of sector OAC
area of sector OBD
Area of the shaded region
{माना OB=r=7cm
और OA=R=14cm
अब, छायांकित भाग का क्षेत्रफल
त्रिज्यखंड OAC का क्षेत्रफल
त्रिज्यखंड OBD का क्षेत्रफल
छायांकित भाग का क्षेत्रफल
}
Q20. Find the area of the shaded region in figure, if the radii of the two concentric circles with centre O are 7cm and 14cm respectively and ∠AOC=40°.
{आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए यदि केंद्र O वाले दोनों संकेंद्रित वृत्तों की त्रिज्याएँ क्रमशः 7cm और 14cm हैं तथा ∠AOC=40° हैं|}
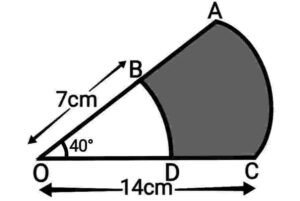
Ans. Let OB=r=7cm
and OC=R=14cm
Now, area of the shaded region
area of sector OAC
area of sector OBD
Area of the shaded region
{माना OB=r=7cm
और OC=R=14cm
अब, छायांकित भाग का क्षेत्रफल
त्रिज्यखंड OAC का क्षेत्रफल
त्रिज्यखंड OBD का क्षेत्रफल
छायांकित भाग का क्षेत्रफल
}
Q21. In the given figure, a square OABC is inscribed in a quadrant OPBQ. If OA=20cm, find the area of the shaded region.
{दी गई आकृति में एक चतुर्थांश OPBQ के अंतर्गत एक वर्ग OABC बना हुआ है| यदि OA=20cm है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए|
}
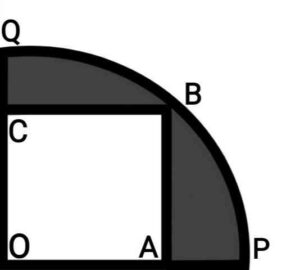
Ans. Join OB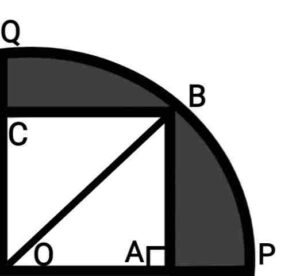 Radius of quadrant=OB
Radius of quadrant=OB
Now, area of the shaded region
area of quadrant OQP
area of square OCBA
Area of the shaded region
{OB को मिलाये  चतुर्थांश की त्रिज्या=OB
चतुर्थांश की त्रिज्या=OB
अब, छायांकित भाग का क्षेत्रफल
चतुर्थांश OQP का क्षेत्रफल
वर्ग OCBA का क्षेत्रफल
छायांकित भाग का क्षेत्रफल
}
Q22. Find the area of the shaded region in the given figure, where a circular arc of radius 6cm has been drawn with vertex O of an equilateral triangle OAB of side 12cm as centre.
{आकृति में छायांकित भाग का क्षेत्रफल ज्ञात करें, जहाँ भुजा 12cm वाले एक समबाहु त्रिभुज OAB के शीर्ष O को केंद्र मानकर 6cm त्रिज्या वाला एक वृत्तीय चाप खींचा गया है|}
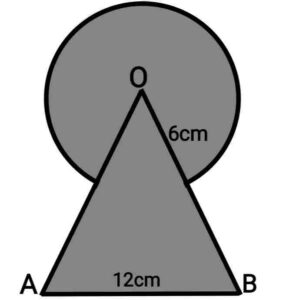
Ans.
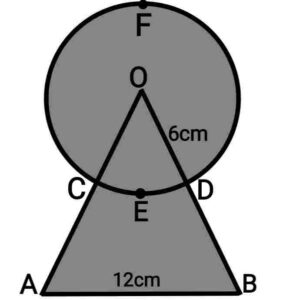 Triangle is equilateral and angle of equilateral triangle=60°.
Triangle is equilateral and angle of equilateral triangle=60°.
Now, area of the shaded region
(area of circle
area of minor sector OCED)
area of equilateral ΔOAB
Area of the shaded region
{ त्रिभुज समबाहु है और समबाहु त्रिभुज का कोण=60°
त्रिभुज समबाहु है और समबाहु त्रिभुज का कोण=60°
अब, छायांकित भाग का क्षेत्रफल
(वृत्त का क्षेत्रफल
लघु त्रिज्यखंड OCED का क्षेत्रफल)
समबाहु ΔOAB का क्षेत्रफल
छायांकित भाग का क्षेत्रफल
}
Q23. AB and CD are respectively arcs of two concentric circles of radii 21cm and 7cm and centre O. If ∠AOB=30°, find the area of the shaded region.
(AB और CD केंद्र O तथा त्रिज्याओं 21cm और 7cm वाले दो संकेंद्रित वृत्तों के क्रमशः दो चाप हैं| यदि ∠AOB=30° है तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए|}
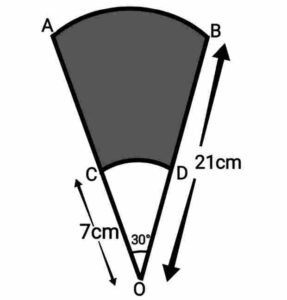
Ans. Let BO=R=21cm
and CO=r=7cm
Now, area of the shaded region
area of sector AOB
area of sector COD
Area of the shaded region
{माना BO=R=21cm
और CO=r=7cm
अब, छायांकित भाग का क्षेत्रफल
त्रिज्यखंड AOB का क्षेत्रफल
त्रिज्यखंड COD का क्षेत्रफल
छायांकित भाग का क्षेत्रफल
}
Q24. Find the area of the shaded region in figure, if ABCD is a square of side 14cm and APD and BPC are two semicircles.
{आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए यदि ABCD भुजा 14cm का एक वर्ग है और APD और BPC दो अर्धवृत्त हैं|}
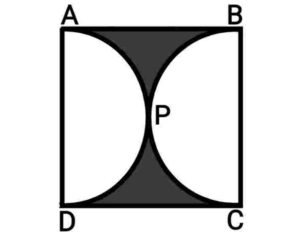
Ans. Side of square=14cm
So, radius(r) of circle
Now, area of shaded region
area of square ABCD
(2×area of semicircles)
Area of the shaded region
{वर्ग की भुजा=14cm
तो, वृत्त की त्रिज्या(r)
अब, छायांकित भाग का क्षेत्रफल
वर्ग ABCD का क्षेत्रफल
(2×अर्धवृत्त का क्षेत्रफल)
छायांकित भाग का क्षेत्रफल
}
Q25. If figure AB and CD are two diameter of a circle(with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA=7cm, find the area of the shaded region.
{आकृति में AB और CD केंद्र O वाले एक वृत्त के दो परस्पर लम्ब व्यास है तथा OD छोटे वृत्त का व्यास है| यदि OA=7cm हैं, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए|}
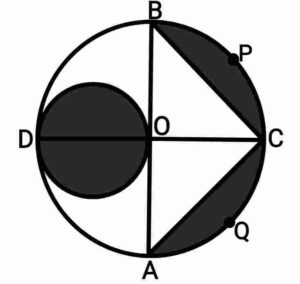
Ans. Radius of big circle=R=7cm
and radius of small circle=r
Now, area of small circle of diameter OD
And, (area of segment BPC area of segment CQA)
area of semicircle BCA
area of triangle BCA
Area of the shaded region
area of small circle
(area of segment BPC
area of segment CQA)
Area of the shaded region
{बड़े वृत्त की त्रिज्या=R=7cm
और छोटे वृत्त की त्रिज्या=r
अब, व्यास OD के छोटे वृत्त का क्षेत्रफल
और, (वृत्तखंड BPC का क्षेत्रफल वृत्तखंड CQA का क्षेत्रफल)
अर्धवृत्त BCA का क्षेत्रफल
त्रिभुज BCA का क्षेत्रफल
छायांकित भाग का क्षेत्रफल
छोटे वृत्त का क्षेत्रफल
(वृत्तखंड BPC का क्षेत्रफल
वृत्तखंड CQA का क्षेत्रफल)
छायांकित भाग का क्षेत्रफल
}
OR
Radius of big circle=R=7cm
and radius of small circle=r
Now, area of small circle of diameter OD
Now, area of segment BPC
area of quadrant OBPC
area of ΔBOC
Similarly, area of segment CQA
Area of the shaded region
area of small circle
area of segment BPC
area of segment CQA
Area of the shaded region
{बड़े वृत्त की त्रिज्या=R=7cm
और छोटे वृत्त की त्रिज्या=r
अब, व्यास OD के छोटे वृत्त का क्षेत्रफल
अब, वृत्तखंड BPC का क्षेत्रफल
चतुर्थांश OBPC का क्षेत्रफल
ΔBOC का क्षेत्रफल
इसी प्रकार, वृत्तखंड CQA का क्षेत्रफल
छायांकित भाग का क्षेत्रफल
छोटे वृत्त का क्षेत्रफल
वृत्तखंड BPC का क्षेत्रफल
वृत्तखंड CQA का क्षेत्रफल
छायांकित भाग का क्षेत्रफल
}
9113323460

I hope you like it. If you like then please share it and you can also Donate to our website by my number and QR code which is given above.
Thanks.
