Statistics (सांख्यिकी)

Get “Statistics” chapter’s previous years questions from 2009 to 2020.

Q1. What do we call the graph which has been drawn between class interval and cumulative frequency?

{वर्ग अंतराल और संचयी बारंबारता के बीच खींचे गए आलेख को क्या कहते हैं?}

year 2019, 2016, 2013 of 1 marks

Ans. Ogive or cumulative frequency curve

{तोरण या संचयी बारंबारता वक्र}

Q2. The cumulative frequency curve is also called …

{संचयी बारंबारता वक्र को … भी कहते हैं|}

year 2018, 2015 of 1 marks

Ans. Ogive

{तोरण}

Q3. What type of ogive do we call a graph which has been drawn between lower limits of class interval and cumulative frequency?

{वर्ग अंतराल की निम्न सीमाओं और संचयी बारंबारता के बीच खींचे गए आलेख को किस प्रकार के तोरण कहते हैं?}

year 2014 of 1 marks

Ans. More than type ogive.

{से अधिक प्रकार का तोरण है|}

Q4. Which type of ogive is it?

{यह किस प्रकार का तोरण है?}

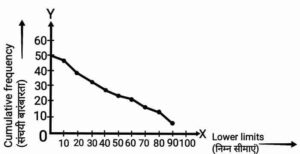
Statistics

year 2020, 2017, 2012 of 1 marks

Ans. More than type ogive.

{से अधिक प्रकार का तोरण है|}

Q5. What type of ogive is the following figure?

{निम्न चित्र किस प्रकार का तोरण है?}

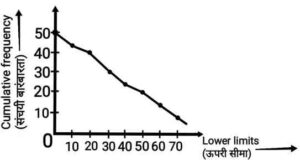
Statistics

year 2009 of 1 marks

Ans. More than type ogive.

{से अधिक प्रकार का तोरण है|}

Q6. What type of ogive is the following figure?

{निम्न चित्र किस प्रकार का तोरण है?}

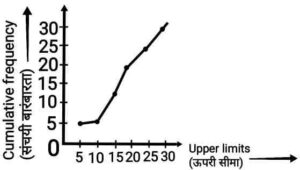
Statistics

year 2010 of 1 marks

Ans. Less than type ogive.

{से कम प्रकार का तोरण है|}

Q7. Write the class interval of the cumulative frequency 20 from the ogive given below.

नीचे दिए गए तोरण से संचयी बारंबारता 20 का वर्ग अंतराल लिखिए|}

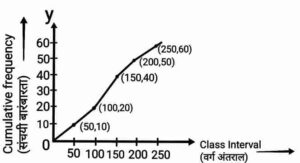
Statistics

year 2011 of 1 marks

Ans. 50-100

Q8. Find the mean of the following data:

Class interval	45-55	55-65	65-75	75-85	85-95
Frequency	3	10	11	8	3

{निम्न आँकड़ो से माध्य ज्ञात कीजिये

वर्ग अंतराल	45-55	55-65	65-75	75-85	85-95
बारंबारता	3	10	11	8	3

}

year 2020 of 6 marks

Ans.

Mean= $\frac{\Sigma f_{i}x_{i}}{\Sigma f_{i}}=\frac{2430}{35}=69.43$

{

माध्य= $\frac{\Sigma f_{i}x_{i}}{\Sigma f_{i}}=\frac{2430}{35}=69.43$ }

Q9. Find the mean of the following data:

Class interval	10-25	25-40	40-55	55-70	70-85	85-100
Frequency	2	3	7	6	6	6

{निम्न आँकड़ो से माध्य ज्ञात कीजिये

वर्ग अंतराल	10-25	25-40	40-55	55-70	70-85	85-100
बारंबारता	2	3	7	6	6	6

}

year 2019 of 6 marks

Ans.

Mean= $\frac{\Sigma f_{i}x_{i}}{\Sigma f_{i}}=\frac{1860}{30}=62$

{

माध्य= $\frac{\Sigma f_{i}x_{i}}{\Sigma f_{i}}=\frac{1860}{30}=62$ }

Q10. Find the median of the following data:

Class interval	0-10	10-20	20-30	30-40	40-50	50-60	60-70
Frequency	5	10	18	30	20	12	5

{निम्न आँकड़ो से माध्यक ज्ञात कीजिये

वर्ग अंतराल	0-10	10-20	20-30	30-40	40-50	50-60	60-70
बारंबारता	5	10	18	30	20	12	5

}

year 2020,2014 of 6 marks

Ans.

Class intertval	Frequency(f)	Cumulative Frequency(cf)
0-10	5	5
10-20	10	15
20-30	18	33
30-40	30	63
40-50	20	83
50-60	12	95
60-70	5	100

Now, $\frac{n}{2}=\frac{100}{2}=50$

30-40 is the class whose cumulative frequency 63 is greater than and nearest to 50.
So, 30-40 is the median class.

Here, l=30, f=30, cf=33 and
h=40-30=10

∴ Median= $l+\left ( \frac{\frac{n}{2}-cf}{f} \right )\times h$

$=30+\left ( \frac{50-33}{30} \right )\times10$

$=30+\left (\frac{17}{30}\times10 \right )$
$=30+5.66=35.66$

{

वर्ग अंतराल	बारंबारता(f)	संचयी बारंबारता(cf)
0-10	5	5
10-20	10	15
20-30	18	33
30-40	30	63
40-50	20	83
50-60	12	95
60-70	5	100

अब, $\frac{n}{2}=\frac{100}{2}=50$

30-40 वह वर्ग है जिसकी संचयी बारंबारता 63 है और वह 50 से अधिक और निकटतम है।
अतः माध्यक वर्ग=30-40

यहाँ, l=30, f=30, cf=33,
और h=40-30=10

∴ माध्यक= $l+\left ( \frac{\frac{n}{2}-cf}{f} \right )\times h$

$=30+\left ( \frac{50-33}{30} \right )\times10$

$=30+\left (\frac{17}{30}\times10 \right )$
$=30+5.66=35.66$ }

Q11. Find the median of the following data:

Class intertval	0-10	10-20	20-30	30-40	40-50	50-60
Frequency	5	8	20	15	7	5

{निम्न आँकड़ो से माध्यक ज्ञात कीजिये

वर्ग अंतराल	0-10	10-20	20-30	30-40	40-50	50-60
बारंबारता	5	8	20	15	7	5

}

year 2019,2009 of 6 marks

Ans.

Class intertval	Frequency(f)	Cumulative Frequency(cf)
0-10	5	5
10-20	8	13
20-30	20	33
30-40	15	48
40-50	7	55
50-60	5	60

Now, $\frac{n}{2}=\frac{60}{2}=30$

20-30 is the class whose cumulative frequency 33 is greater than and nearest to 30.
So, 20-30 is the median class.

Here, l=20, f=20, cf=13 and
h=30-20=10

∴ Median= $l+\left ( \frac{\frac{n}{2}-cf}{f} \right )\times h$

$=20+\left ( \frac{30-13}{20} \right )\times 10$

$=20+\frac{17}{2}=20+8.5=28.5$

{

वर्ग अंतराल	बारंबारता(f)	संचयी बारंबारता(cf)
0-10	5	5
10-20	8	13
20-30	20	33
30-40	15	48
40-50	7	55
50-60	5	60

अब, $\frac{n}{2}=\frac{60}{2}=30$

20-30 वह वर्ग है जिसकी संचयी बारंबारता 33 है और वह 30 से अधिक और निकटतम है।
अतः माध्यक वर्ग=20-30

यहाँ, l=20, f=20, cf=13 और
h=30-20=10

∴ माध्यक= $l+\left ( \frac{\frac{n}{2}-cf}{f} \right )\times h$

$=20+\left ( \frac{30-13}{20} \right )\times 10$

$=20+\frac{17}{2}=20+8.5=28.5$ }

Q12. Find the median of the following data:

Class interval	40-45	45-50	50-55	55-60	60-65	65-70	70-75
Frequency	2	3	8	6	6	3	2

{निम्न आँकड़ो से माध्यक ज्ञात कीजिये

वर्ग अंतराल	40-45	45-50	50-55	55-60	60-65	65-70	70-75
बारंबारता	2	3	8	6	6	3	2

}

year 2018,2015,2012 of 6 marks

Ans.

Class interval	Frequency(f)	Cumulative Frequency(cf)
40-45	2	2
45-50	3	5
50-55	8	13
55-60	6	19
60-65	6	25
65-70	3	28
70-75	2	30

Now, $\frac{n}{2}=\frac{30}{2}=15$

55-60 is the class whose cumulative frequency 19 is greater than and nearest to 15.
So, 55-60 is the median class.

Here, l=55, f=6, cf=13 and
h=60-55=5

∴ Median= $This image has an empty alt attribute; its file name is gif.latex$

$=55+\left ( \frac{15-13}{6} \right )\times 5$

$=55+\left ( \frac{2}{6} \times5\right )=55+1.67=56.67$

{

वर्ग अंतराल	बारंबारता(f)	संचयी बारंबारता(cf)
40-45	2	2
45-50	3	5
50-55	8	13
55-60	6	19
60-65	6	25
65-70	3	28
70-75	2	30

अब, $\frac{n}{2}=\frac{30}{2}=15$

55-60 वह वर्ग है जिसकी संचयी बारंबारता 19 है और वह 15 से अधिक और निकटतम है।
अतः माध्यक वर्ग=55-60

यहाँ, l=55, f=6, cf=13 और
h=60-55=5

∴ माध्यक= $This image has an empty alt attribute; its file name is gif.latex$

$=55+\left ( \frac{15-13}{6} \right )\times 5$

$=55+\left ( \frac{2}{6} \times5\right )=55+1.67=56.67$ }

Q13. Find the median of the following data:

Class interval	65-85	85-105	105-125	125-145	145-165	165-185	185-205
Frequency	4	5	13	20	14	8	4

{निम्न आँकड़ो से माध्यक ज्ञात कीजिये

वर्ग अंतराल	65-85	85-105	105-125	125-145	145-165	165-185	185-205
बारंबारता	4	5	13	20	14	8	4

}

year 2013 of 6 marks

Ans.

Class interval	Frequency(f)	Cumulative Frequency(cf)
65-85	4	4
85-105	5	9
105-125	13	22
125-145	20	42
145-165	14	56
165-185	8	64
185-205	4	68

Now, $\frac{n}{2}=\frac{68}{2}=34$

125-145 is the class whose cumulative frequency 42 is greater than and nearest to 34.
So, 125-145 is the median class.

Here, l=125, f=20, cf=22 and
h=145-125=20

∴ Median= $This image has an empty alt attribute; its file name is gif.latex$

$=125+\left ( \frac{34-22}{20} \right )\times20$

$=125+12=137$

{

वर्ग अंतराल	बारंबारता(f)	संचयी बारंबारता(cf)
65-85	4	4
85-105	5	9
105-125	13	22
125-145	20	42
145-165	14	56
165-185	8	64
185-205	4	68

अब, $\frac{n}{2}=\frac{68}{2}=34$

यहाँ, l=125, f=20, cf=22 और
h=145-125=20

∴ माध्यक= $This image has an empty alt attribute; its file name is gif.latex$

$=125+\left ( \frac{34-22}{20} \right )\times20$

$=125+12=137$ }

Q14 Find the mode of the following data:

Class interval	65-85	85-105	105-125	125-145	145-165	165-185	185-205
Frequency	4	5	13	20	14	8	4

{निम्न आँकड़ो से बहुलक ज्ञात कीजिये

वर्ग अंतराल	65-85	85-105	105-125	125-145	145-165	165-185	185-205
बारंबारता	4	5	13	20	14	8	4

}

year 2016,2010 of 6 marks

Ans. The maximum class frequency is 20.
So, modal class=125-145,

Here, l=125, f₁=20, f₂=14, f₀=13,
h=145-125=20

∴ Mode= $l+\left ( \frac{f_{1}-f_{0}}{2f_{1}-f_{0}-f_{2}} \right )\times h$

$=125+\left ( \frac{20-13}{2\times20-13-14} \right )\times 20$

$=125+\left ( \frac{7}{13} \times20\right )$
$=125+10.76=135.76$

{अधिकतम वर्ग बारंबारता 20 है|
तो, बहुलक वर्ग=125-145,

यहाँ, l=125, f₁=20, f₂=14, f₀=13,
h=145-125=20

∴ बहुलक= $l+\left ( \frac{f_{1}-f_{0}}{2f_{1}-f_{0}-f_{2}} \right )\times h$

$=125+\left ( \frac{20-13}{2\times20-13-14} \right )\times 20$

$=125+\left ( \frac{7}{13} \times20\right )$
$=125+10.76=135.76$ }

Q15. Find the mean or median (any one) of the following data:

Class interval	65-85	85-105	105-125	125-145	145-165	165-185	185-205
Frequency	4	5	13	20	14	8	4

{निम्न आँकड़ो से माध्य अथवा माध्यक (कोई एक) ज्ञात कीजिये

वर्ग अंतराल	65-85	85-105	105-125	125-145	145-165	165-185	185-205
बारंबारता	4	5	13	20	14	8	4

}

year 2017 of 6 marks

Ans.

MEAN

Mean= $\frac{\Sigma f_{i}x_{i}}{\Sigma f_{i}}=\frac{9320}{68}=137.05$

OR

MEDIAN

Class interval	Frequency(f)	Cumulative Frequency(cf)
65-85	4	4
85-105	5	9
105-125	13	22
125-145	20	42
145-165	14	56
165-185	8	64
185-205	4	68

Now, $\frac{n}{2}=\frac{68}{2}=34$

125-145 is the class whose cumulative frequency 42 is greater than and nearest to 34.
So, 125-145 is the median class

Here, l=125, f=20, cf=22 and
h=145-125=20

∴ Median= $This image has an empty alt attribute; its file name is gif.latex$

$=125+\left ( \frac{34-22}{20} \right )\times20$

$=125+12=137$

{

माध्य

माध्य= $\frac{\Sigma f_{i}x_{i}}{\Sigma f_{i}}=\frac{9320}{68}=137.05$

OR

माध्यक

वर्ग अंतराल	बारंबारता(f)	संचयी बारंबारता(cf)
65-85	4	4
85-105	5	9
105-125	13	22
125-145	20	42
145-165	14	56
165-185	8	64
185-205	4	68

अब, $\frac{n}{2}=\frac{68}{2}=34$

125-145 वह वर्ग है जिसकी संचयी बारंबारता 42 है और वह 34 से अधिक और निकटतम है।
अतः माध्यक वर्ग=125-145

यहाँ, l=125, f=20, cf=22 और h=145-125=20

∴ माध्यक= $This image has an empty alt attribute; its file name is gif.latex$

$=125+\left ( \frac{34-22}{20} \right )\times20$

$=125+12=137$ }

Q16. A life insurance agent found the following data for the distribution of ages of 100 policy folders. Determine the median age, if policies are only given the persons having age 18 years onwards but less than 60 years.

Ages(in years)	Numbers of policy holders
Below 20	2
Below 25	6
Below 30	24
Below 35	45
Below 40	78
Below 45	89
Below 50	92
Below 55	98
Below 60	100

{एक जीवन बीमा एजेंट 100 पॉलिसी धारकों की आयु के बंटन के निम्नलिखित आँकड़े ज्ञात करता है| माध्यिका आयु ज्ञात कीजिये, यदि पॉलिसी केवल उन्हीं व्यक्तियों को दी जाती हैं, जिनकी आयु 18 वर्ष या उससे अधिक हो, परन्तु 60 वर्ष से कम हो|}

आयु(वर्षों में)	पॉलिसी धारकों की संख्या
20 से कम	2
25 से कम	6
30 से कम	24
35 से कम	45
40 से कम	78
45 से कम	89
50 से कम	92
55 से कम	98
60 से कम	100

year 2011 of 6 marks

Ans.

Class interval	Frequency(f)	Cumulative Frequency(cf)
Below 20	2	2
20-25	4	6
25-30	18	24
30-35	21	45
35-40	33	78
40-45	11	89
45-50	3	92
50-55	6	98
55-60	2	100

Now, $\frac{n}{2}=\frac{100}{2}=50$

35-40 is the class whose cumulative frequency 78 is greater than and nearest to 50.
So, 35-40 is the median class.

Here, l=35, f=33, cf=45 and
h=40-35=5

∴ Median= $l+\left ( \frac{\frac{n}{2}-cf}{f} \right )\times h$

$=35+\left ( \frac{50-45}{33} \right )\times5$

$=35+\left ( \frac{25}{33} \right )$
$=35+0.76=35.76$

{

वर्ग अंतराल	बारंबारता(f)	संचयी बारंबारता(cf)
20 से कम	2	2
20-25	4	6
25-30	18	24
30-35	21	45
35-40	33	78
40-45	11	89
45-50	3	92
50-55	6	98
55-60	2	100

अब, $\frac{n}{2}=\frac{100}{2}=50$

35-40 वह वर्ग है जिसकी संचयी बारंबारता 78 है और वह 50 से अधिक और निकटतम है।
अतः माध्यक वर्ग=35-40

यहाँ, l=35, f=33, cf=45 और
h=40-35=5

∴ माध्यक= $l+\left ( \frac{\frac{n}{2}-cf}{f} \right )\times h$

$=35+\left ( \frac{50-45}{33} \right )\times5$

$=35+\left ( \frac{25}{33} \right )$
$=35+0.76=35.76$ }

9113323460

Paytm

I hope you like it. If you like then please share it and you can also Donate to our website by my number and QR code which is given above.

Thanks.

Class interval	Frequency(f_i)	Class-mark(x_i)	[Frequency×Class-mark](f_ix_i)
45-55	3	50	150
55-65	10	60	600
65-75	11	70	770
75-85	8	80	640
85-95	3	90	270
Total	$\Sigma f_{i}=35$		$\Sigma f_{i}x_{i}=2430$

वर्ग अंतराल	बारंबारता(f_i)	वर्ग चिह्न(x_i)	[बारंबारता×वर्ग चिह्न](f_ix_i)
45-55	3	50	150
55-65	10	60	600
65-75	11	70	770
75-85	8	80	640
85-95	3	90	270
योग	$\Sigma f_{i}=35$		$\Sigma f_{i}x_{i}=2430$

Class intertval	Frequency(f_i)	Class-mark(x_i)	[Frequency×Class-mark](f_ix_i)
10-25	2	17.5	35
25-40	3	32.5	97.5
40-55	7	47.5	332.5
55-70	6	62.5	375
70-85	6	77.5	465
85-100	6	92.5	555
Total	$\Sigma f_{i}=30$		$\Sigma f_{i}x_{i}=1860$

वर्ग अंतराल	बारंबारता(f_i)	वर्ग चिह्न(x_i)	[बारंबारता×वर्ग चिह्न](f_ix_i)
10-25	2	17.5	35
25-40	3	32.5	97.5
40-55	7	47.5	332.5
55-70	6	62.5	375
70-85	6	77.5	465
85-100	6	92.5	555
योग	$\Sigma f_{i}=30$		$\Sigma f_{i}x_{i}=1860$

Class interval	Frequency(f_i)	Class-mark(x_i)	[Frequency×Class-mark](f_ix_i)
65-85	4	75	300
85-105	5	95	475
105-125	13	115	1495
125-145	20	135	2700
145-165	14	155	2170
165-185	8	175	1400
185-205	4	195	780
Total	$\Sigma f_{i}=68$		$\Sigma f_{i}x_{i}=9320$

STUDENTHAPPY

Statistics (सांख्यिकी)

Statistics (सांख्यिकी)

MEAN