Coordinate geometry (निर्देशांक ज्यामिति)
Get “Coordinate geometry” chapter’s previous years questions from 2009 to 2020 of JAC board.
Q1. Find the distance between the points A(-5,7) and B(-1,3)
{बिंदुओं A(-5,7) और B(-1,3) के बीच की दूरी ज्ञात कीजिए|}
Ans. From distance formula,
units
{दुरी सूत्र से,
मात्रक}
Q2. Find the distance between the points A(2,3) and B(4,1)
{बिंदुओं A(2,3) और B(4,1) के बीच की दूरी ज्ञात कीजिए|}
Ans. From distance formula,
{दुरी सूत्र से,
मात्रक}
Q3. Find the distance between the points A(a,b) and B(-a,-b)
{बिंदुओं A(a,b) और B(-a,-b) के बीच की दूरी ज्ञात कीजिए|}
Ans. From distance formula,
units
{दुरी सूत्र से,
मात्रक}
Q4. Find the value of y which the distance between the points P(2,-3) and Q(10,y) is 10 units.
{y का मान ज्ञात कीजिए जिसके लिए बिंदु P(2,-3) और Q(10,y) के बीच की दूरी 10 मात्रक है|}
Ans. PQ = 10
After squaring,
or
y=6-3 or y= -6-3
y=3 or y= -9
∴ y=3,-9
{PQ = 10
वर्ग करने पर ,
या
y=6-3 या y= -6-3
y=3 या y= -9
∴ y=3,-9}
Q5. Find the point on the y-axis which is equidistant from (6,5) and (-4,3)
{y-अक्ष पर वह बिंदु ज्ञात कीजिये जो (6,5) और (-4,3) से समदूरस्थ है|}
Ans. Let the point be P(0,y) which is equidistant from A(6,5) and B(-4,3)
∴ AP=PB
Squaring both side,
∴ point=(0,9)
{माना की वह बिंदु P(0,y) है जो A(6,5) और B(-4,3) से समदूरस्थ है|
∴ AP=PB
दोनों तरफ वर्ग करने पर ,
∴ बिंदु=(0,9) }
Q6. Find the point on the x-axis which is equidistant from (2,5) and (-2,9)
{x-अक्ष पर वह बिंदु ज्ञात कीजिये जो (2,5) और (-2,9) से समदूरस्थ है|}
Ans Let the point be P(x,0) which is equidistant from A(2,5) and B(-2,9)
∴ AP=PB
Squaring both side,
∴ point=(-7,0)
{माना की वह बिंदु P(x,0) है जो A(2,5) और B(-2,9) से समदूरस्थ है|
∴ AP=PB
दोनों तरफ वर्ग करने पर,
∴ बिंदु=(-7,0) }
Q7. Find the co-ordinates of the points which divides the segment joining the points (4,-3) and (8,5) in the ratio 3:1 internally.
{उस बिंदु के निर्देशांक ज्ञात कीजिए जो बिंदुओं (4,-3) और (8,5) को जोड़ने वाले रेखाखंड को आंतरिक रुप में 3:1 के अनुपात में विभाजित करता है|}
Ans. Lets the co-ordinates of the point is P(x,y)
Using section formula
∴ the co-ordinates of the points is (7,3)
{माना की बिंदु का निर्देशांक P(x,y) है|
विभाजन सूत्र से,
∴ बिंदु का निर्देशांक (7,3) है|}
Q8. Find the co-ordinates of the points which divides the segment joining the points A(-1,7) and B(4,-3) in the ratio 2:3.
{उस बिंदु के निर्देशांक ज्ञात कीजिए जो बिंदुओं A(-1,7) और B(4,-3) को जोड़ने वाले रेखाखंड को 2:3 के अनुपात में विभाजित करता है|}
Ans. Lets the co-ordinates of the point is P(x,y)
Using section formula
∴ the co-ordinates of the points is (1,3)
{माना की बिंदु का निर्देशांक P(x,y) है|
विभाजन सूत्र से,
∴ बिंदु का निर्देशांक (1,3) है|}
Q9. Find out the co-ordinates of a point A, where AB is a diameter of a circle whose centre is (2,-3) and B is (1,4)
{बिंदु A का निर्देशांक ज्ञात कीजिए जहां AB एक वृत्त का व्यास है जिसका केंद्र (2,-3) है तथा B के निर्देशांक (1,4) हैं}
Ans. 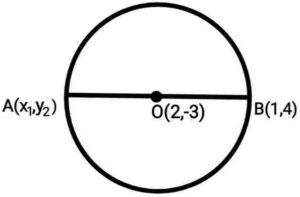 Let the co-ordinates of a point A be
Let the co-ordinates of a point A be
Now,
{ माना की बिंदु A का निर्देशांक
माना की बिंदु A का निर्देशांक
अब,
}
Q10. Find the ratio in which the y-axis divides the line segment joining the points (5,-6) and (-1,-4).
{बिंदुओं (5,-6) और (-1,-4) को जोड़ने वाले रेखाखंड को y-अक्ष किस अनुपात में विभाजित करती है|}
Ans. Let the co-ordinates of the point is P(0,y) and ratio be k:1
Then by using section formula,
Ratio= k:1 =5:1
OR
Lets the co-ordinates of the point is P(0,y) and ratio be m:n
now,
or
∴ m:n=5:1
{माना की बिंदु का निर्देशांक P(0,y) और अनुपात k:1 है|
विभाजन सूत्र से,
अनुपात = k:1 = 5:1
OR
माना की बिंदु का निर्देशांक P(0,y) है|
अब,
या
∴ m:n=5:1}
Q11. In what ratio does the point(-4,6) divides the line segment joining the points A(-6,10) and B(3,-8)
{बिंदु (-4,6), बिन्दुओ A(-6,10) और B(3,-8) को जोड़ने वाले रेखाखंड को किस अनुपात में विभाजित करता है|}
Ans. Let the ratio be k:1
Then by using section formula,
Ratio =k:1 =
:1 =2:7
OR
Let the ratio be m:n
∴
∴ m:n=2:7
{माना की अनुपात k:1 है|
विभाजन सूत्र से,
अनुपात =k:1 =
:1 =2:7
OR
माना की अनुपात m:n हैं|
∴
∴ m:n=2:7}
Q12. If the point A(6,1), B(8,2), C(9,4) and D(p,3) are the vertices of a parallelogram, taken in order. Then find the value of p
{ यदि बिंदु A(6,1), B(8,2), C(9,4) और D(p,3) एक समांतर चतुर्भुज के शीर्ष इसी क्रम में हो, तो p का मान ज्ञात कीजिए}
Ans.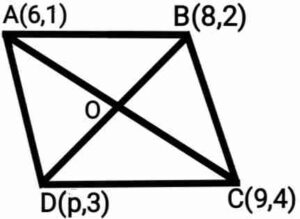 We know that diagonals of a parallelogram bisect each other
We know that diagonals of a parallelogram bisect each other
So, the coordinates of the midpoint of AC=coordinates of the midpoint of BD
∴ p=7
{ समांतर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं
समांतर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं
विकर्ण AC के मध्य बिंदु के निर्देशांक=विकर्ण BD के मध्य बिंदु के निर्देशांक
∴ p=7}
Q13. Find the area of triangle , the co-ordinates of whose vertices are (-5,-1), (3,-5) and (5,2)
{त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसमें शीर्षों के निर्देशांक (-5,-1), (3,-5) और (5,2) है|}
Ans. Area of triangle
{त्रिभुज का क्षेत्रफल
वर्ग मात्रक}
Q14. Find the area of triangle , the co-ordinates of whose vertices are (1,-1), (-4,6) and (-3,-5)
{त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसमें शीर्षों के निर्देशांक (1,-1), (-4,6) और (-3,-5) है|}
Ans. Area of triangle
sq.unit
{त्रिभुज का क्षेत्रफल
वर्ग मात्रक}
Q15. Find the area of triangle , the co-ordinates of whose vertices are P(-1.5,3), Q(6,-2) and R(-3,4)
{त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसमें शीर्षों के निर्देशांक P(-1.5,3), Q(6,-2) और R(-3,4) है|}
Ans. Area of triangle
{त्रिभुज का क्षेत्रफल
}
Q16. Find the area of triangle , the co-ordinates of whose vertices are A(5,2), B(4,7) and C(7,-4)
{त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसमें शीर्षों के निर्देशांक A(5,2), B(4,7) और C(7,-4) है|}
Ans. Area of triangle
Area will always positive
∴ Area=2 sq.unit
{त्रिभुज का क्षेत्रफल
क्षेत्र हमेशा सकारात्मक रहेगा
∴ क्षेत्र=2 वर्ग मात्रक}
Q17. Find the value of k for which the following points are collinear: (8,1), (k,-4), (2,-5)
{k का मान ज्ञात कीजिए ताकि निम्न तीनों बिंदुएं संरेखी हो (8,1), (k,-4), (2,-5)}
Ans. If the given points are collinear then the area of triangle formed by them must be 0
i.e.,
{तीनों बिंदुएं संरेखी हो तो त्रिभुज का क्षेत्रफल 0 होगा|
अर्थात्,
}
Q18. Find the value of k for which the following points are collinear: (7,-2), (5,1), (3,k)
{k का मान ज्ञात कीजिए ताकि निम्न तीनों बिंदुएं संरेखी हो (7,-2), (5,1), (3,k)}
Ans. If the given points are collinear then the area of triangle formed by them must be 0
i.e.,
{तीनों बिंदुएं संरेखी हो तो त्रिभुज का क्षेत्रफल 0 होगा|
अर्थात्,
}
Q19. Find the value of k for which the following points are collinear: A(2,3), B(4,k), and C(6,-3)
{k का मान ज्ञात कीजिए ताकि निम्न तीनों बिंदुएं संरेखी हो A(2,3), B(4,k), और C(6,-3)}
Ans. If the given points are collinear then the area of triangle formed by them must be 0
i.e.,
∴ k = 0
{तीनों बिंदुएं संरेखी हो तो त्रिभुज का क्षेत्रफल 0 होगा|
अर्थात्,
∴ k = 0}
Q20. Find the area of rhombus if its vertex are (3,0), (4,-5), (-1,4) and (-2,-1) taken in order.
{एक समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष इसी क्रम में (3,0), (4,-5), (-1,4) और (-2,-1) हैं|}
Ans. 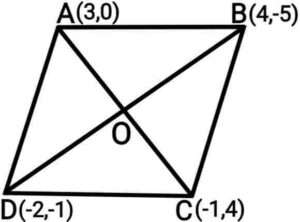
And,
Now, area of rhombus ABCD= ×product of diagonals
square unit
Area of rhombus ABCD
square unit
{

और,
अब, समचतुर्भुज ABCD का क्षेत्रफल= ×विकर्णों का गुणनफल
वर्ग मात्रक
समचतुर्भुज ABCD का क्षेत्रफल
वर्ग मात्रक}
Q21. If A and B are (-2,-2) and (2,-4) respectively, find the coordinate of P such that and P lies on the line segment AB.
{यदि A और B क्रमशः (-2,-2) और (2,-4) हैं तो बिंदु P का निर्देशांक ज्ञात कीजिए ताकि हो और P रेखाखंड AB पर स्थित हो|}
Ans. 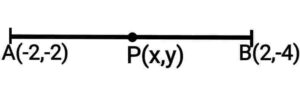
Using section formula,
Coordinate of P
{
विभाजन सूत्र से,
P का निर्देशांक
}
Q22. If the distances of P(x,y) from points A(3,6) and B(-3,4) are equal, prove that 3x+y=5.
{यदि P(x,y) की दूरी बिंदु A(3,6) और B(-3,4) से समान है, तो सिद्ध कीजिए कि 3x+y=5}
Ans. 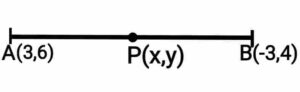 Given:- AP=PB
Given:- AP=PB
Squaring both side,
{ दिया हुआ है:- AP=PB
दिया हुआ है:- AP=PB
दोनों तरफ वर्ग करने पर,
}
Q23. If A(-5,7), B(-4,-5), C(-1,-6) and D(4,5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD.
{यदि A(-5,7), B(-4,-5), C(-1,-6) और D(4,5) एक चतुर्भुज ABCD के शीर्ष हैं, तो इस चतुर्भुज का क्षेत्रफल ज्ञात कीजिए|}
Ans. 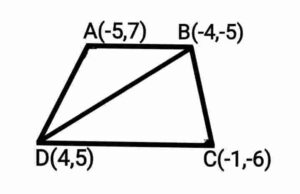 ar(ΔABD)
ar(ΔABD)
square units.
Now, ar(ΔBCD)
square units
Area of the quadrilateral ABCD =ar(ΔABD)+ar(ΔBCD)
=53+19=72 square units
{ ar(ΔABD)
ar(ΔABD)
वर्ग मात्रक
अब, ar(ΔBCD)
वर्ग मात्रक
चतुर्भुज ABCD का क्षेत्रफल =ar(ΔABD)+ar(ΔBCD)
=53+19=72 वर्ग मात्रक}
Q24. Find out a relation between x and y such that the point (x,y) is equidistant from the points (3,6) and (-3,-4).
{x और y में एक ऐसा संबंध ज्ञात कीजिए कि बिंदु (x,y) बिंदुओं (3,6) और (-3,-4) से समदूरस्थ हो|}
Ans. 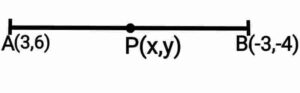 Given:- AP=PB
Given:- AP=PB
Squaring both side,
{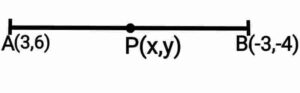 दिया हुआ है:- AP=PB
दिया हुआ है:- AP=PB
दोनों तरफ वर्ग करने पर,
}
Q25. Find out the area of triangle formed by joining the midpoint of the sides of the triangle ABC whose vertices are (0,-1), (2,1) and (0,3). Find the ratio of the area of the triangle ABC formed to the area of the given triangle.
{शीर्षों (0,-1), (2,1) और (0,3) वाले त्रिभुज की भुजाओं के मध्य बिंदुओं से बनने वाले त्रिभुज का क्षेत्रफल ज्ञात कीजिए| इस क्षेत्रफल का दिए हुए त्रिभुज के क्षेत्रफल के साथ अनुपात ज्ञात कीजिए|}
Ans.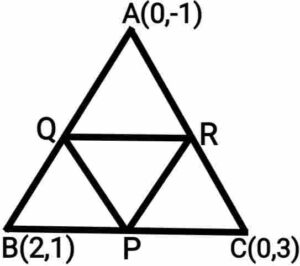 Coordinate of P
Coordinate of P
, Coordinate of Q
and Coordinate of R
Now, ar(ΔPQR)
Area≠negative
ar(ΔPQR)=1 square units.
and ar(ΔABC)
ar(ΔABC)=4 square units.
{ P का निर्देशांक
P का निर्देशांक
, Q का निर्देशांक
और R का निर्देशांक
अब, ar(ΔPQR)
क्षेत्रफल≠नकारात्मक
ar(ΔPQR)=1 वर्ग मात्रक
और ar(ΔABC)
ar(ΔABC)=4 वर्ग मात्रक
}
9113323460

I hope you like it. If you like then please share it and you can also Donate to our website by my number and QR code which is given above.
Thanks.
