Pair of linear equations in two variables (दो चर वाले रैखिक समीकरण युग्म)

Get “Pair of linear equations in two variables” chapter’s previous years questions from 2009 to 2020 of JAC board.

Q1. Solve {हल कीजिये}

$x-y=3$

$\frac{x}{3}+\frac{y}{2}=6$

year 2019 of 3 marks

Ans. $x-y=3$ …(1)

and $\frac{x}{3}+\frac{y}{2}=6$ …(2)

[Equation(1)×½] + equation(2)

$\Rightarrow\frac{x}{2}+\frac{x}{3}=\frac{3}{2}+6$

$\Rightarrow\frac{3x+2x}{6}=\frac{3+12}{2}$

$\Rightarrow \frac{3x+2x}{3} = 15$

$\Rightarrow 5x=45$

$\Rightarrow x=9$

Putting the value of x in equation(1)

$\Rightarrow$ 9 – y =3 $\Rightarrow$ y = 9 – 3 =6

∴ x = 9 and y = 6

{ $x-y=3$ …(1)

और $\frac{x}{3}+\frac{y}{2}=6$ …(2)

समीकरण(1) को ½ से गुणा कर समीकरण(2) में जोड़ने पर

$\Rightarrow\frac{x}{2}+\frac{x}{3}=\frac{3}{2}+6$

$\Rightarrow\frac{3x+2x}{6}=\frac{3+12}{2}$

$\Rightarrow \frac{3x+2x}{3} = 15$

$\Rightarrow 5x=45$

$\Rightarrow x=9$

x का मान समीकरण(1) में रखने पर

$\Rightarrow$ 9 – y =3 $\Rightarrow$ y = 9 – 3 =6

∴ x = 9 and y = 6}

Q2. Solve {हल कीजिये}

$\frac{3x}{2}-\frac{5y}{3}=-2$ and $\frac{x}{3}+\frac{y}{2}=\frac{13}{6}$

year 2018, 2015, 2013 of 3 marks

Ans. $\frac{3x}{2}-\frac{5y}{3}=-2$ …(1)

$\frac{x}{3}+\frac{y}{2}=\frac{13}{6}$ …(2)

Now, in eq(1)
$\frac{3x}{2}-\frac{5y}{3}=-2$

$\Rightarrow\frac{9x-10y}{6}=-2$

$\Rightarrow{9x-10y}=-12$ …(3)

and eq(2)
$\frac{x}{3}+\frac{y}{2}=\frac{13}{6}$

$\Rightarrow\frac{2x+3y}{6}=\frac{13}{6}$

$\Rightarrow{2x+3y}={13}$ …(4)

Now, [equation (3) × 3] + [equation(4) × 10]

$\Rightarrow$ 47x = 94

$\Rightarrow$ x = 2

Putting the value of x in equation (4)

$\Rightarrow$ (2×2) +3y =13

$\Rightarrow$ 4 + 3y = 13

$\Rightarrow$ 3y = 13 – 4

$\Rightarrow$ y = 3

∴ x = 2 and y = 3

{ $\frac{3x}{2}-\frac{5y}{3}=-2$ …(1)

$\frac{x}{3}+\frac{y}{2}=\frac{13}{6}$ …(2)

अब, समीकरण(1) में
$\frac{3x}{2}-\frac{5y}{3}=-2$

$\Rightarrow\frac{9x-10y}{6}=-2$

$\Rightarrow{9x-10y}=-12$ …(3)

और समीकरण(2) में
$\frac{x}{3}+\frac{y}{2}=\frac{13}{6}$

$\Rightarrow\frac{2x+3y}{6}=\frac{13}{6}$

$\Rightarrow{2x+3y}={13}$ …(4)

[समीकरण (3) × 3] + [समीकरण (4) × 10]

$\Rightarrow$ 47x = 94

$\Rightarrow$ x = 2

x का मान समीकरण (4) में रखने पर

$\Rightarrow$ (2×2) +3y =13

$\Rightarrow$ 4 + 3y = 13

$\Rightarrow$ 3y = 13 – 4

$\Rightarrow$ y = 3

∴ x = 2 and y = 3}

Q3. Solve graphically.
{ग्राफीय विधि से हल कीजिए|}

y=6-2x , y=2x-2

year 2020 of 3 marks

Ans. Solutions of y=6-2x

x	0	1
y=6-2x	6	4

And, solutions of y=2x-2

x	0	1
y=2x-2	-2	0

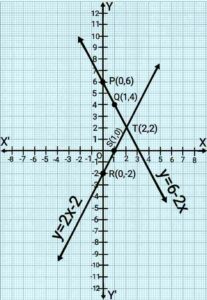
Pair of linear equations in two variables
Here, 1 square=1 unit.

Point T(2,2) is common to both the lines PQ and RS.
$\therefore$ Solution of pair of linear equations is x=2 and y=2.

{y=6-2x के हल

x	0	1
y=6-2x	6	4

और y=2x-2 के हल

x	0	1
y=2x-2	-2	0

Pair of linear equations in two variables

यहाँ, 1 वर्ग=1 इकाई

रेखाओं PQ और RS में एक उभयनिष्ठ बिंदु T(2,2) है|
$\therefore$ रैखिक समीकरणों के युग्म का हल x=2 और y=2 है|}

Q4. Solve graphically.
{ग्राफीय विधि से हल कीजिए|}

2x-y=2 , 4x-y=4

year 2019, 2017, 2015 of 3 marks

Ans. Solutions of 2x-y=2

x	0	1
y=2x-2	-2	0

And, solutions of 4x-y=4

x	0	1
y=4x-4	-4	0

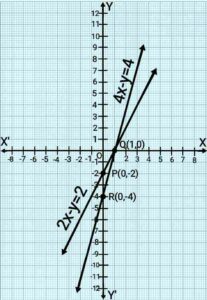Pair of linear equations in two variables Here, 1 square=1 unit.

Point Q(1,0) is common to both the lines PQ and RQ.
$\therefore$ Solution of pair of linear equations is x=1 and y=0.

{2x-y=2 के हल

x	0	1
y=2x-2	-2	0

और 4x-y=4 के हल

x	0	1
y=4x-4	-4	0

Pair of linear equations in two variables

यहाँ, 1 वर्ग=1 इकाई

रेखाओं PQ और RQ में एक उभयनिष्ठ बिंदु Q(1,0) है|
$\therefore$ रैखिक समीकरणों के युग्म का हल x=1 और y=0 है|}

Q5. Solve graphically.
{ग्राफीय विधि से हल कीजिए|}

2x+y=6 , 2x-y=2

year 2018, 2010 of 3 marks

Ans. Solutions of 2x+y=6

x	0	1
y=6-2x	6	4

And, solutions of 2x-y=2

x	0	1
y=2x-2	-2	0

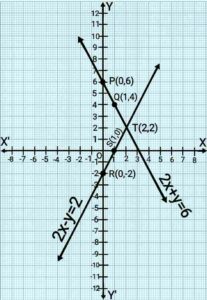
Pair of linear equations in two variables
Here, 1 square=1 unit.

Point T(2,2) is common to both the lines PQ and RS.
$\therefore$ Solution of pair of linear equations is x=2 and y=2.

{2x+y=6 के हल

x	0	1
y=6-2x	6	4

और 2x-y=2 के हल

x	0	1
y=2x-2	-2	0

Pair of linear equations in two variables यहाँ, 1 वर्ग=1 इकाई

Q6. Solve graphically.
{ग्राफीय विधि से हल कीजिए|}

x+y=10 , y-x=4

year 2016, 2014 of 3 marks

Ans. Solutions of x+y=10

x	0	1
y=10-x	10	9

And, solutions of y-x=4

x	0	1
y=4+x	4	5

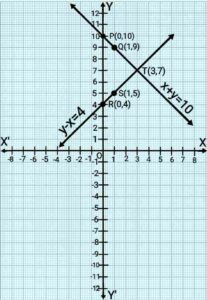Pair of linear equations in two variables Here, 1 square=1 unit

Point T(3,7) is common to both the lines PQ and RS.
$\therefore$ Solution of pair of linear equations is x=3 and y=7.

{x+y=10 के हल

x	0	1
y=10-x	10	9

और y-x=4 के हल

x	0	1
y=4+x	4	5

Pair of linear equations in two variables यहाँ, 1 वर्ग=1 इकाई

रेखाओं PQ और RS में एक उभयनिष्ठ बिंदु T(3,7) है|
$\therefore$ रैखिक समीकरणों के युग्म का हल x=3 और y=7 है|}

Q7. Solve graphically.
{ग्राफीय विधि से हल कीजिए|}

x-2y=0 , 3x+4y=20

year 2013 of 3 marks

Ans. Solutions of x-2y=0

And, solutions of 3x+4y=20

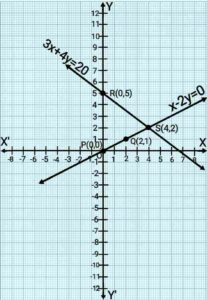Pair of linear equations in two variables Here, 1 square=1 unit

Point S(4,2) is common to both the lines PQ and RS.
$\therefore$ Solution of pair of linear equations is x=4 and y=2.

{x-2y=0 के हल

और 3x+4y=20 के हल

Pair of linear equations in two variables यहाँ, 1 वर्ग=1 इकाई

रेखाओं PQ और RS में एक उभयनिष्ठ बिंदु S(4,2) है|
$\therefore$ रैखिक समीकरणों के युग्म का हल x=4 और y=2 है|}

Q8. Check whether the following pairs of linear equations are inconsistent or consistent. If consistent obtain the solution graphically:
2x+y-6=0, 4x-2y-4=0

{निम्न रैखिक समीकरणों के युग्म संगत हैं या नहीं, जाँच कीजिए| यदि संगत हैं तो ग्राफीय विधि से हल कीजिए:
2x+y-6=0, 4x-2y-4=0}

year 2012 of 3 marks

Ans. $\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}$ and $\frac{b_1}{b_2}=\frac{1}{-2}$

$\therefore \; \frac{a_1}{a_2}\not =\frac{b_1}{b_2}$

$\therefore$ Pair of linear equations are consistent and have unique solution.

Solutions of 2x+y-6=0

Solutions of 4x-2y-4=0

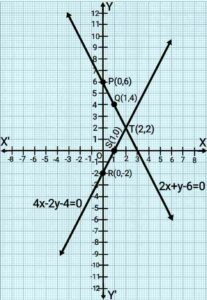
Here, 1 square=1 unit.

Point T(2,2) is common to both the lines PQ and RS.
$\therefore$ Solution of pair of linear equations is x=2 and y=2.

{ $\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}$ और $\frac{b_1}{b_2}=\frac{1}{-2}$

$\therefore \; \frac{a_1}{a_2}\not =\frac{b_1}{b_2}$

$\therefore$ रैखिक समीकरणों के युग्म संगत हैं और अद्वितीय हल प्राप्त होंगे|

2x+y-6=0 के हल

और 4x-2y-4=0 के हल

यहाँ, 1 वर्ग=1 इकाई

Q9. Check whether the pairs of equations x+3y=6 and 2x-3y=12 are consistent. If so, solve them graphically:

{जाँच कीजिए कि समीकरण युग्म x+3y=6 और 2x-3y=12 संगत है| यदि ऐसा है, तो उन्हें ग्राफ द्वारा हल कीजिए|}

year 2011, 2009 of 3 marks

Ans. $\frac{a_1}{a_2}=\frac{1}{2}$ and $\frac{b_1}{b_2}=\frac{3}{-3}=-1$

$\therefore \; \frac{a_1}{a_2}\not =\frac{b_1}{b_2}$

$\therefore$ Pair of linear equations are consistent and have unique solution.

Solutions of x+3y=6

Solutions of 2x-3y=12

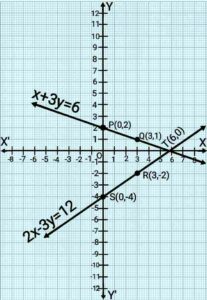
Pair of linear equations in two variables

Here, 1 square=1 unit.

Point T(6,0) is common to both the lines PQ and SR.
$\therefore$ Solution of pair of linear equations is x=6 and y=0.

{ $\frac{a_1}{a_2}=\frac{1}{2}$ और $\frac{b_1}{b_2}=\frac{3}{-3}=-1$

$\therefore \; \frac{a_1}{a_2}\not =\frac{b_1}{b_2}$

$\therefore$ रैखिक समीकरणों के युग्म संगत हैं और अद्वितीय हल प्राप्त होंगे|

x+3y=6 के हल

और 2x-3y=12 के हल

Pair of linear equations in two variables

यहाँ, 1 वर्ग=1 इकाई

रेखाओं PQ और SR में एक उभयनिष्ठ बिंदु T(6,0) है|
$\therefore$ रैखिक समीकरणों के युग्म का हल x=6 और y=0 है|}

Q10. Solve:
हल कीजिये:

$\begin{aligned}\frac{2}{x}+\frac{3}{y}=13\\ \frac{5}{x}-\frac{4}{y}=-2\end{aligned}$

year 2020, 2016, 2014, 2012 of 3 marks

Ans. $\begin{aligned}\frac{2}{x}+\frac{3}{y}=13\\ \frac{5}{x}-\frac{4}{y}=-2\end{aligned}$

Let $\frac{1}{x}=u\; ,\; \frac{1}{y}=v$

$\therefore \; \begin{aligned}2u+3v=13\; ...(i)\\ \5u-4v=-2\; ...(ii)\end{aligned}$

$Now,\; [eq^n(i)\times4]+[eq^n(ii)\times3]$

$\begin{aligned}8u+12v=52\, \,\\ \frac{15u-12v=-6}{23u=46}\end{aligned}$

$\Rightarrow u=\frac{46}{23}=2$

$Putting\; the\; value\; of\; u\; in\; eq^n(i)$
$2\times2+3v=13$
$\Rightarrow 3v=13-4=9$
$\Rightarrow v=\frac{9}{3}=3$

Now, u=2 and v=3

$\because$ $\frac{1}{x}=u\; ,\; \frac{1}{y}=v$

$\Rightarrow \frac{1}{x}=2\; ,\; \frac{1}{y}=3$

$\Rightarrow x=\frac{1}{2}\; ,\; y=\frac{1}{3}$

$\therefore \; x=\frac{1}{2}\; ,\; y=\frac{1}{3}$

{

$\begin{aligned}\frac{2}{x}+\frac{3}{y}=13\\ \frac{5}{x}-\frac{4}{y}=-2\end{aligned}$

माना की $\frac{1}{x}=u\; ,\; \frac{1}{y}=v$

$\therefore \; \begin{aligned}2u+3v=13\; ...(i)\\ \5u-4v=-2\; ...(ii)\end{aligned}$

अब, $[eq^n(i)\times4]+[eq^n(ii)\times3]$

$\begin{aligned}8u+12v=52\, \,\\ \frac{15u-12v=-6}{23u=46}\end{aligned}$

$\Rightarrow u=\frac{46}{23}=2$

u का मान $eq^n(i)$ में रखने पर
$2\times2+3v=13$
$\Rightarrow 3v=13-4=9$
$\Rightarrow v=\frac{9}{3}=3$

अब, u=2 और v=3
$\because$ $\frac{1}{x}=u\; ,\; \frac{1}{y}=v$

$\Rightarrow \frac{1}{x}=2\; ,\; \frac{1}{y}=3$

$\Rightarrow x=\frac{1}{2}\; ,\; y=\frac{1}{3}$

$\therefore \; x=\frac{1}{2}\; ,\; y=\frac{1}{3}$ }

Q11. Solve:
हल कीजिये:

$\begin{aligned}\frac{4}{x}+3y=14\\ \frac{3}{x}-4y=23\end{aligned}$

year 2017 of 3 marks

Ans. $\begin{aligned}\frac{4}{x}+3y=14\\ \frac{3}{x}-4y=23\end{aligned}$

$Let\; \: \frac{1}{x}=u$

$\therefore$ $\begin{aligned}{4}{u}+{3}{y}=14\; ...(i)\\ {3}{u}-{4}{y}=23\; ...(ii)\end{aligned}$

$Now,\; [eq^n(i)\times4]+[eq^n(ii)\times3]$

$\begin{aligned}16u+12y=56\\ \frac{9u-12y=69}{25u=125}\end{aligned}$

$\Rightarrow u=\frac{125}{25}=5$

$Putting\; the\; value\; of\; u\; in\; eq^n(i)$
$4\times5+3y=14$
$\Rightarrow 3y=14-20$
$\Rightarrow y=\frac{-6}{3}=-2$

$Now,\; \because \frac{1}{x}=u$

$\Rightarrow \frac{1}{x}=5$

$\Rightarrow x= \frac{1}{5}$

$\therefore x=\frac{1}{5}\: ,y=-2$

{

$\begin{aligned}\frac{4}{x}+3y=14\\ \frac{3}{x}-4y=23\end{aligned}$

माना की, $\frac{1}{x}=u$

$\therefore$ $\begin{aligned}{4}{u}+{3}{y}=14\; ...(i)\\ {3}{u}-{4}{y}=23\; ...(ii)\end{aligned}$

अब, $[eq^n(i)\times4]+[eq^n(ii)\times3]$

$\begin{aligned}16u+12y=56\\ \frac{9u-12y=69}{25u=125}\end{aligned}$

$\Rightarrow u=\frac{125}{25}=5$

u का मान $eq^n(i)$ में रखने पर
$4\times5+3y=14$
$\Rightarrow 3y=14-20$
$\Rightarrow y=\frac{-6}{3}=-2$

अब, $\because \frac{1}{x}=u$

$\Rightarrow \frac{1}{x}=5$

$\Rightarrow x= \frac{1}{5}$

$\therefore x=\frac{1}{5}\: ,y=-2$ }

Q12. Solve:
हल कीजिये:

$\begin{aligned}\frac{2}{\sqrt{x}}+\frac{3}{\sqrt{y}}=2\\ \frac{4}{\sqrt{x}}-\frac{9}{\sqrt{y}}=-1\end{aligned}$

year 2010 of 3 marks

Ans. $\begin{aligned}\frac{2}{\sqrt{x}}+\frac{3}{\sqrt{y}}=2\\ \frac{4}{\sqrt{x}}-\frac{9}{\sqrt{y}}=-1\end{aligned}$

$Let,$ $\frac{1}{\sqrt{x}}=u\; ,\; \frac{1}{\sqrt{y}}=v$

$\therefore \; \begin{aligned}2u+3v=2\; ...(i)\\ 4u-9v=-1\; ...(ii)\end{aligned}$

$Now,$ $[eq^n(i)\times3]+[eq^n(ii)]$

$\begin{aligned}6u+9v=6\;\;\; \\ \frac{4u-9v=-1}{10u=5}\end{aligned}$

$\Rightarrow u=\frac{5}{10}=\frac{1}{2}$

$Putting\; the\; value\; of\; u\; in\; eq^n(i)$

$2\times\frac{1}{2}+3v=2$
$\Rightarrow 3v=2-1=1$
$\Rightarrow v=\frac{1}{3}$

$Now,$ $u=\frac{1}{2}\; ,\; v=\frac{1}{3}$

$\because$ $\frac{1}{\sqrt{x}}=u\; ,\; \frac{1}{\sqrt{y}}=v$

$\Rightarrow \frac{1}{\sqrt{x}}=\frac{1}{2}\; ,\; \frac{1}{\sqrt{y}}=\frac{1}{3}$
$\Rightarrow \sqrt{x}=2\; ,\; \sqrt{y}=3$
$\Rightarrow x=4\; ,\; y=9$

$\therefore x=4\; ,\; y=9$

{

$\begin{aligned}\frac{2}{\sqrt{x}}+\frac{3}{\sqrt{y}}=2\\ \frac{4}{\sqrt{x}}-\frac{9}{\sqrt{y}}=-1\end{aligned}$

माना की, $\frac{1}{\sqrt{x}}=u\; ,\; \frac{1}{\sqrt{y}}=v$

$\therefore \; \begin{aligned}2u+3v=2\; ...(i)\\ 4u-9v=-1\; ...(ii)\end{aligned}$

अब, $[eq^n(i)\times3]+[eq^n(ii)]$

$\begin{aligned}6u+9v=6\;\;\; \\ \frac{4u-9v=-1}{10u=5}\end{aligned}$

$\Rightarrow u=\frac{5}{10}=\frac{1}{2}$

u का मान $eq^n(i)$ में रखने पर

$2\times\frac{1}{2}+3v=2$
$\Rightarrow 3v=2-1=1$
$\Rightarrow v=\frac{1}{3}$

अब, $u=\frac{1}{2}\; ,\; v=\frac{1}{3}$

$\because$ $\frac{1}{\sqrt{x}}=u\; ,\; \frac{1}{\sqrt{y}}=v$

$\Rightarrow \frac{1}{\sqrt{x}}=\frac{1}{2}\; ,\; \frac{1}{\sqrt{y}}=\frac{1}{3}$
$\Rightarrow \sqrt{x}=2\; ,\; \sqrt{y}=3$
$\Rightarrow x=4\; ,\; y=9$

$\therefore x=4\; ,\; y=9$ }

Q13. Solve:
हल कीजिये:

$\begin{aligned}6x+3y=6xy\\ 2x+4y=5xy\end{aligned}$

year 2009 of 3 marks

Ans. Given:- 6x+3y=6xy
Dividing both side by xy
$\frac{6x}{xy}+\frac{3y}{xy}=\frac{6xy}{xy}$

$\Rightarrow \frac{6}{y}+\frac{3}{x}=6\; ...(i)$

And, 2x+4y=5xy
Dividing both side by xy
$\frac{2x}{xy}+\frac{4y}{xy}=\frac{5xy}{xy}$

$\Rightarrow \frac{2}{y}+\frac{4}{x}=5\; ...(ii)$

Let $\frac{1}{x}=u\; ,\; \frac{1}{y}=v$

From eq(i) and eq(ii)

$\begin{aligned}6v+3u=6\; ...(iii)\\ 2v+4u=5\; ...(iv)\end{aligned}$

$Now,$ $[eq^n(iii)\times4]-[eq^n(iv)\times3]$

$\begin{aligned}24v+12u=24\\ 6v+12u=15\\ \frac{-\;\; \; \;-\;\; \; \; \;\,\; \;\: -\;\; }{18v=9} \end{}$

$\Rightarrow v=\frac{9}{18}=\frac{1}{2}$

Putting the value of v in eq(iii)

$6\times\frac{1}{2}+3u=6$
$\Rightarrow 3u=6-3=3$
$\Rightarrow u=\frac{3}{3}=1$

$Now,$ $\Rightarrow u=1\; ,\; v=\frac{1}{2}$

$\because$ $\frac{1}{x}=u\; ,\; \frac{1}{y}=v$

$\Rightarrow \frac{1}{x}=1\; ,\; \frac{1}{y}=\frac{1}{2}$
$\Rightarrow {x}=1\; ,\; {y}={2}$

$\therefore \; {x}=1\; ,\; {y}={2}$

{दिया गया है:- 6x+3y=6xy
दोनों तरफ xy से विभाजित करने पर

$\frac{6x}{xy}+\frac{3y}{xy}=\frac{6xy}{xy}$

$\Rightarrow \frac{6}{y}+\frac{3}{x}=6\; ...(i)$

और , 2x+4y=5xy
दोनों तरफ xy से विभाजित करने पर

$\frac{2x}{xy}+\frac{4y}{xy}=\frac{5xy}{xy}$

$\Rightarrow \frac{2}{y}+\frac{4}{x}=5\; ...(ii)$

माना की $\frac{1}{x}=u\; ,\; \frac{1}{y}=v$

eq(i) और eq(ii) से

$\begin{aligned}6v+3u=6\; ...(iii)\\ 2v+4u=5\; ...(iv)\end{aligned}$

अब, $[eq^n(iii)\times4]-[eq^n(iv)\times3]$

$\begin{aligned}24v+12u=24\\ 6v+12u=15\\ \frac{-\;\; \; \;-\;\; \; \; \;\,\; \;\: -\;\; }{18v=9} \end{}$

$\Rightarrow v=\frac{9}{18}=\frac{1}{2}$

v का मान eq(iii) में रखने पर

$6\times\frac{1}{2}+3u=6$
$\Rightarrow 3u=6-3=3$
$\Rightarrow u=\frac{3}{3}=1$

अब, $\Rightarrow u=1\; ,\; v=\frac{1}{2}$

$\because$ $\frac{1}{x}=u\; ,\; \frac{1}{y}=v$

$\Rightarrow \frac{1}{x}=1\; ,\; \frac{1}{y}=\frac{1}{2}$
$\Rightarrow {x}=1\; ,\; {y}={2}$

$\therefore \; {x}=1\; ,\; {y}={2}$

Q14. A boat goes 44 km downstream and 30 km upstream in 10 hours. In 13 hours, it can go 55 km downstream and 40 km upstream. Find out the speed of the stream and that of the boat in the still water.

{एक नाव 10 घंटे में धारा के प्रतिकूल 30 किमी तथा धारा के अनुकूल 44 किमी जाती है| 13 घंटे में वह 40 किमी धारा के प्रतिकूल एवं 55 किमी धारा के अनुकूल जाती है| धारा की चाल तथा नाव की स्थिर पानी में चाल ज्ञात कीजिए|}

year 2011 of 3 marks

Ans. Let the speed of the boat in still water be x km/h
and speed of the stream be y km/h

Then, the speed of boat in upstream =(x-y) km/h
and speed of boat in downstream =(x+y) km/h

Now, time to cover 44km downstream+time to cover 30km upstream=10hrs
$i.e,\; \frac{44}{x+y}+\frac{30}{x-y}=10\; ...(i)$

and, time to cover 55km downstream+time to cover 40km upstream=13hrs
$i.e,\; \frac{55}{x+y}+\frac{40}{x-y}=13\; ...(ii)$

$Let\; \, \frac{1}{x+y}=u\; and\; \frac{1}{x-y}=v$

From $eq^n(i)$ and $eq^n(ii)$
$\begin{aligned}44u+30v=10\; ...(iii)\\ 55u+40v=13\; ...(iv) \end{}$

$Now,$ $[eq^n(iii)\times4]-[eq^n(iv)\times3]$

$\begin{aligned}176u+120v=40\\ 165u+120v=39\\ \frac{-\;\; \; \; \;\, \;-\;\; \; \; \;\,\; \;\: \; \; \; -\; }{11u=1} \end{}$

$\Rightarrow u=\frac{1}{11}$

Putting the value of u in $eq^n(iii)$
$44\times\frac{1}{11}+30v=10$
$\Rightarrow 30v=10-4$
$\Rightarrow v=\frac{6}{30}=\frac{1}{5}$

$Now,$ $u=\frac{1}{11}\;,\; v=\frac{1}{5}$

$\because \; \frac{1}{x+y}=u\; ,\; \frac{1}{x-y}=v$

$\Rightarrow \frac{1}{x+y}=\frac{1}{11}\;,\; \frac{1}{x-y}=\frac{1}{5}$
$\Rightarrow \; {x+y}=11\; ,\; {x-y}=5$

$Now,$ $(x+y)+(x-y)=11+5$
$\Rightarrow 2x=16$
$\Rightarrow x=8$

$\because\; x+y=11$
$\Rightarrow 8+y=11$
$\Rightarrow y=11-8=3$

Hence, the speed of the boat in still water be 8 km/h
and speed of the stream be 3 km/h.

{माना शांत जल में नाव की चाल x किमी/घण्टा है
और धारा की गति y किमी/घंटा है

तो, धारा के प्रतिकूल नाव की गति =(x-y) km/h
और धारा के अनुकूल नाव की गति =(x+y) km/h

अब, धारा के अनुकूल 44 किमी की दूरी तय करने का समय+धारा के प्रतिकूल 30 किमी की दूरी तय करने का समय=10घंटे $i.e,\; \frac{44}{x+y}+\frac{30}{x-y}=10\; ...(i)$

और, धारा के अनुकूल 55 किमी की दूरी तय करने का समय+धारा के प्रतिकूल 40 किमी की दूरी तय करने का समय=13घंटे $i.e,\; \frac{55}{x+y}+\frac{40}{x-y}=13\; ...(ii)$

माना की, $\frac{1}{x+y}=u\; ,\; \frac{1}{x-y}=v$

$eq^n(i)$ और $eq^n(ii)$ से
$\begin{aligned}44u+30v=10\; ...(iii)\\ 55u+40v=13\; ...(iv) \end{}$

अब, $[eq^n(iii)\times4]-[eq^n(iv)\times3]$

$\begin{aligned}176u+120v=40\\ 165u+120v=39\\ \frac{-\;\; \; \; \;\, \;-\;\; \; \; \;\,\; \;\: \; \; \; -\; }{11u=1} \end{}$

$\Rightarrow u=\frac{1}{11}$

u का मान $eq^n(iii)$ में डालने पर,
$44\times\frac{1}{11}+30v=10$
$\Rightarrow 30v=10-4$
$\Rightarrow v=\frac{6}{30}=\frac{1}{5}$

अब, $u=\frac{1}{11}\;,\; v=\frac{1}{5}$

$\because \; \frac{1}{x+y}=u\; ,\; \frac{1}{x-y}=v$

$\Rightarrow \frac{1}{x+y}=\frac{1}{11}\;,\; \frac{1}{x-y}=\frac{1}{5}$
$\Rightarrow \; {x+y}=11\; ,\; {x-y}=5$

अब, $(x+y)+(x-y)=11+5$
$\Rightarrow 2x=16$
$\Rightarrow x=8$

$\because\; x+y=11$
$\Rightarrow 8+y=11$
$\Rightarrow y=11-8=3$

अत: शांत जल में नाव की चाल 8 किमी/घण्टा होगी
और धारा की गति 3 किमी/घंटा होगी|

9113323460

Paytm

I hope you like it. If you like then please share it and you can also Donate to our website by my number and QR code which is given above.

Thanks.

STUDENTHAPPY

Pair of linear equations in two variables (दो चर वाले रैखिक समीकरण युग्म)